Basamak Kavramı Çözümlü Örnek Soruları
Örnek:
A ile B birer rakam, AB ve BA da iki basamaklı sayılardır.Buna göre, AB – BA farkı aşağıdakilerden hangisi olamaz?
A) 9 B) 18 C) 36 D) 54 E) 61
Çözüm:

Yanıt E
Örnek:
A, B, C birer rakam AB iki basamaklı bir sayı ve
AB – (A + B + C) = 47
olduğuna göre, A kaçtır?
A)5 B)6 C)7 D)8 E)9
Çözüm:

Yanıt B
Örnek:
ab ve ba iki basamaklı doğal sayılardır.
ab = 5(a + b)
olduğuna göre, ba doğal sayısı rakamları toplamının kaç katıdır?
A) 2 B) 4 C) 6 D) 8 E) 10
Çözüm:
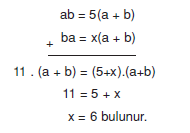
Yanıt C
Örnek:
Üç basamaklı abc doğal sayısının yüzler basamağındaki rakam ile onlar basamağındaki rakam yer değiştirdiğinde sayının değeri 720 artmaktadır.
Buna göre, a + b + c toplam›n›n en büyük de¤eri kaçt›r?
A) 11 B) 13 C) 15 D) 17 E) 19
Çözüm:
abc sayısının yüzler basamağı ile onlar basamağındaki rakamlar yer değiştirirse bac sayısı elde edilir
bac – abc = 720
100b + 10a + c – 100a – 10b – c = 720
90b – 90a = 720
90.(b–a) = 720
b(9) – a(1) = 8
c sayısı ise 0, 1, 2, …,9 rakamlarından herhangi biri olabilir.
O halde, a + b + c toplamı en çok: 1 + 9 + 9 = 19 dur
Yanıt E
Örnek:
abc ve acb üç basamaklı doğal sayılardır.
abc – acb = 36
olduğuna göre, kaç farklı abc sayısı yazılabilir?
A) 24 B) 34 C) 44 D) 54 E) 64
Çözüm:

Yanıt D
Örnek:
İki basamaklı bir doğal sayının onlar basamağındaki rakam 5 artırılıp, birler basamağındaki rakam 2 azaltılırsa elde edilen sayı, başlangıçtaki sayının 4 katının 6 eksiği oluyor.
Buna göre, başlangıçtaki sayının rakamları çarpımı kaçtır?
A) 4 B) 5 C) 6 D) 7 E) 8
Çözüm:
(ab) + 50 – 2 = 4.(ab) – 6
(ab) + 48 = 4.(ab) – 6
54 = 3.(ab)
ab = 18 dir.
O halde, a.b çarpımı 1.8 = 8 bulunur.
Yanıt E
Örnek:
xy4 ve 6xy üç basamaklı doğal sayılardır.
3.(xy4) – 21 = 6xy
olduğuna göre, iki basamaklı xy sayısı, rakamların toplamının kaç katıdır?
A) 9 B) 8 C) 7 D) 6 E) 5
Çözüm:
3.(xy4) – 21 = 6xy
3.(10.(xy) + 4) – 21 = 6xy
30.(xy) + 12 – 21 = 600 + (xy)
29.(xy) = 609
xy = 21
O halde, 21 sayısı, rakamları toplamının 21 : 3 = 7 katıdır.
Cevap C
[ad1]
Örnek:
ab ve cd iki basamaklı doğal sayılarında a rakamının 4 artırılıp, c rakamının 4 azaltılmasıyla oluşan sayıların çarpımı, ab ile cd nin çarpımından 400 küçüktür.
Buna göre, cd sayısı ab sayısından ne kadar büyüktür?
A) 15 B) 20 C) 25 D) 30 E) 35
Çözüm:
(ab).(cd)–(ab+40).(cd–40)=400
(ab).(cd)–(ab).(cd)+40(ab)–40(cd)+1600=400
40[(ab) – (cd)] = –1200
(ab)–(cd) = –30
cd–ab =30 olur.
O halde, cd sayısı ab say›s›ndan 30 fazladır.
Cevap D
Örnek:
A, B, C birer rakam olmak üzere,
C < B < A
koşulunu sağlayan kaç tane üç basamaklı ABC sayısı vardır?
A) 72 B) 81 C) 90 D) 108 E) 120
Çözüm:
0, 1, 2, …, 9 rakamlarından herhangi 3 tanesini seçtiğimiz
zaman C < B < A olacak şekilde üç basamaklı ABC
sayısı oluşturabiliriz. Buna göre, C < B < A koşulunu sağlayan üç basamaklı ABC sayıları
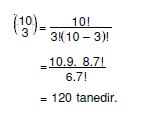
Yanıt E
[m2]
Örnek:
Birbirinden farklı, iki basamaklı üç doğal sayının toplamı A dır.
Buna göre, A kaç farklı değer alabilir?
A) 262 B) 264 C) 266 D) 268 E) 270
Çözüm:
Birbirinden farklı iki basamaklı üç doğal sayının toplamı
en az : 10 + 11 + 12 = 33
en çok : 97 + 98 + 99 = 294 tür.
Diğer iki basamaklı üç doğal sayının toplamı 33 ile 294 arasındadır. Buna göre, 33 ≤ A ≤ 294 olacak şekilde 294 – 33 + 1 = 262 farklı değer alabilir.
Yanıt A
[matematik_1_ygs]

Emeğe saygı _ teşekkürler.
BASİT DEĞİLMİ BUNLAR YGS DE DAHA ZORLARI ÇIKIYOR.
aynen öyle çok basitler
siz ne düşünüyorsunuz
çok çalışmam lazım
ben zor değil sınav tarzı sorular