Dikdörtgenler Prizması, Kare Prizma ve Küpün Yüzey Alanı
Prizmaların yüzey alanı tüm yüzlerinin alanlarının toplamına eşittir. Prizmaların yüzey alanları “A” ile gösterilir.
Dikdörtgenler Prizmasının Yüzey Alanı
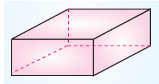
Dikdörtgenler prizmasının 6 yüzü vardır. Bu yüzlerin her biri birer dikdörtgensel bölgedir.
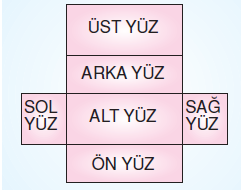
Ön yüz alanı = Arka yüz alanı
Üst yüz alanı = Alt yüz alanı
Sağ yüz alanı = Sol yüz alanı
Dikdörtgenler prizmasının yüzey alanı tüm yüzlerinin alanları toplamına eşittir.
Örnek Soru
Yukarıda verilen dikdörtgenler prizmasının yüzey alanı kaç cm2’dir?
![]()
Cevap
Dikdörtgenler prizmasının altı yüzünün
alanlarını ayrı ayrı bularak toplayalım.
Ön yüz alanı = 10 . 4 = 40 cm2
Arka yüz alanı = 10 . 4 = 40 cm2
Üst yüz alanı = 10 . 6 = 60 cm2
Alt yüz alanı = 10 . 6 = 60 cm2
Sağ yüz alanı = 6 . 4 = 24 cm2
Sol yüz alanı = 6 . 4 = 24 cm2
A = 40 + 40 + 60 + 60 + 24 + 24
A = 80 + 120 + 48 = 248 cm2’dir.
O halde Dikdörtgenler prizmasının yüzey
alanı 248 cm2’dir.
Yanıt A
Örnek Soru
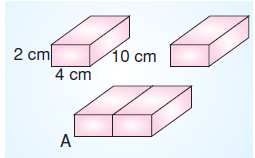
Mert birbirine eş olan iki dikdörtgenler prizmasını birleştirerek A şeklini oluşturuyor.
Buna göre, A şeklinin yüzey alanı kaç cm2’dir?
![]()
Cevap
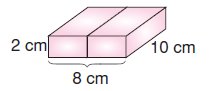
Mert’in iki prizmasıyı birleştirilerek oluşturduğu şekil de bir dikdörtgenler prizmasıdır.
Ön yüz alanı = 8 . 2 = 16 cm2
Arka yüz alanı = 8 . 2 = 16 cm2
Üst yüz alanı = 10 . 8 = 80 cm2
Alt yüz alanı = 10 . 8 = 80 cm2
Sağ yüz alanı = 10 . 2 = 20 cm2
Sol yüz alanı = 10 . 2 = 20 cm2
A = 16 + 16 + 80 + 80 + 20 + 20
A = 32 + 160 + 40 = 232 cm2’dir.
Yanıt D
Örnek Soru
Yukarıda verilen dikdörtgenler prizmasının ön yüz alanı, sağ yüz alanı ve üst yüz alanı sırasıyla 16 cm2, 22 cm2 ve 30 cm2’dir.
Buna göre, bu prizmanın yüzey alanı kaç cm2’dir?
![]()
Ön yüz alanı = Arka yüz alanı = 16 cm2
Sağ yüz alanı = Sol yüz alanı = 22 cm2
Üst yüz alanı = Alt yüz alanı = 30 cm2
A = 16 + 16 + 22 + 22 + 30 + 30
A = 32 + 44 + 60 = 136 cm2 olur.
Yanıt B
Örnek Soru
Boyutları 2 m, 4 m ve 5 m olan dikdörtgenler prizması şeklindeki havuzun iç yüzeyi bir kenarı 40 cm olan kare şeklindeki fayanslarla döşenecektir.
Bu iş için kaç tane fayans gereklidir?
![]()
Cevap
Sağ yüz alanı = 2.4 = 8 m2
Sol yüz alanı = 2.4 = 8 m2
Ön yüz alanı = 2.5 = 10 m2
Arka yüz alanı = 2.5 = 10 m2
Alt yüz alanı = 4.5 = 20 m2
Havuzun iç yüzeyinin alanı
8 + 8 + 10 + 10 + 20 = 56 m2’dir.
56 m2 = 560000 cm2 olur.
Kullanılan fayanslardan bir tanesinin alanı 40.40 = 1600 cm2’dir.
Kaç tane fayans gerektiğini bulmak için iç yüzey alanını fayanslardan birinin alanına bölmeliyiz.

Örnek Soru
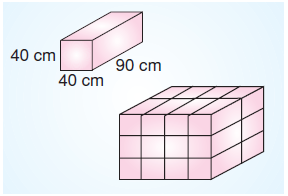
Bir tanesinin boyutları 40 cm, 40 cm, 90 cm olan kare prizma şeklindeki demir parçaları üst üste ve arka arkaya gelecek
şekilde diziliyor. Bu şekilde dizilen parçaların üzerine yağmurdan etkilenmemesi için naylon örtülüyor.
Demir parçalarının üzerini örten naylon parçasının alanı kaç cm2’dir?
![]()
Cevap
Demir parçalarını birleştirerek oluşturulan prizmanın taban ayrıtları 160 cm, 180 cm ve yüksekliği 120 cm’dir.
Naylonun alanını hesaplamak için prizmanın alt yüzü hariç diğer bütün yüzlerinin alanını bulmalıyız.
Üst yüz alanı = 160.180 = 28800 cm2
Sağ yüz alanı = 120.180 = 21600 cm2
Sol yüz alanı = 120.180 = 21600 cm2
Ön yüz alanı = 120.160 = 19200 cm2
Arka yüz alanı = 120.160 = 19200 cm2
Naylonun alanı 28800+21600+21600 +19200+19200 = 110400 cm2’dir.
Yanıt A
Örnek Soru
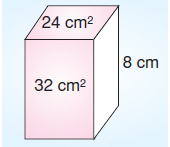
Şekildeki dikdörtgenler prizmasının üst yüzeyinin alanı 24 cm2, ön yüzeyinin alanı 32 cm2 ve yüksekliği 8 cm olduğuna göre, bu prizmanın yüzey alanı kaç cm2’dir?
![]()
Cevap
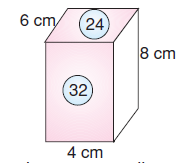
8 . a = 32 ise a = 4 cm’dir.
4 . b = 24 ise b = 6 cm’dir.
Ön yüz alanı = Arka yüz alanı = 32 cm2
Üst yüz alanı = Alt yüz alanı = 24 cm2
Sağ yüz alanı = 8 . 6 = 48 cm2
Sol yüz alanı = 8 . 6 = 48 cm2
A = 32 + 32 + 24 + 24 + 48 + 48
A = 64 + 48 + 96 = 208 cm2 olur.
Yanıt C
Örnek Soru
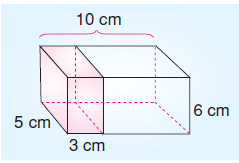
Şekildeki dikdörtgenler prizmasından boyalı kısım kesilip çıkarılıyor.
Buna göre, kalan şeklin alanı kaç cm2 olur?
![]()
Cevap
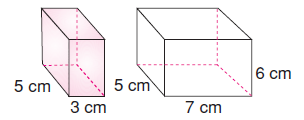
Boyalı kısım çıkarılınca kalan şeklin taban ayrıtı 7 cm olur.
Ön yüz alanı = 7 . 6 = 42 cm2
Arka yüz alanı = 7 . 6 = 42 cm2
Üst yüz alanı = 7 . 5 = 35 cm2
Alt yüz alanı = 7 . 5 = 35 cm2
Sağ yüz alanı = 6 . 5 = 30 cm2
Sol yüz alanı = 6 . 5 = 30 cm2
A = 42 + 42 + 35 + 35 + 30 + 30
A = 84 + 70 + 60 = 214 cm2’dir.
Yanıt D
Örnek Soru
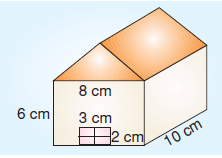
Yukarıda bir öğrencinin kartondan yaptığı okul modeli verilmiştir. Bu okul modelinin yan yüzeyleri boyanacaktır.
Buna göre, boyanacak kısmın yüzey alanı kaç cm2’dir?
![]()
Cevap
Sağ yüz alanı = 10 . 6 = 60 cm2
Sol yüz alanı = 10 . 6 = 60 cm2
Ön yüz alanı = 8 . 6 = 48 cm2
Arka yüz alanı = 8 . 6 = 48 cm2
Kapının yüzey alanı = 3 . 2 = 6 cm2
A = 60 + 60 + 48 + 48 = 216 cm2’dir.
Boyanacak yüzeyin alanı
216 – 6 = 210 cm2 olur.
Yanıt A
Kare Prizamasının Yüzey Alanı
Kare prizmanın 6 yüzü vardır. Kare prizmanın alt ve yüz yüzleri karesel bölge, diğer yüzleri dikdörtgensel bölgedir.
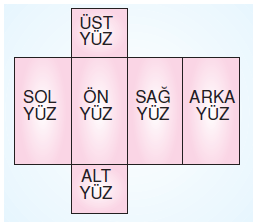
Ön yüz alanı = Arka yüz alanı
Üst yüz alanı = Alt yüz alanı
Sağ yüz alanı = Sol yüz alanı
Kare prizmanın yüzey alanı tüm yüzlerinin alanları toplamına eşittir.
Örnek Soru
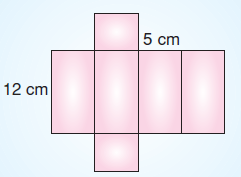
Yukarıda açınımı verilen kare prizmanın yüzey alanı kaç cm2’dir?
![]()
Cevap
Üst yüz alanı = Alt yüz alan› = 5.5 = 25 cm2
Sağ yüz alanı = Sol yüz alan› = 5.12 = 60 cm2
Ön yüz alanı = Arka yüz alan› = 5.12 = 60 cm2
Kare prizman›n yüzey alanı A = 2.25 + 2.60 + 2.60 = 50 + 120 + 120 = 290 cm2’dir.
Yanıt D
Örnek Soru
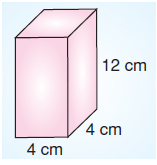
Yukarıda verilen kare prizmanın yüzey alan kaç cm2’dir?
![]()
Cevap
Ön yüz alanı = Arka yüz alanı = 4.12 = 48 cm2
Alt yüz alanı = Üst yüz alanı = 4.4 = 16 cm2
Sağ yüz alanı = Sol yüz alanı = 4.12 = 48 cm2
Kare prizmanın yüzey alanı A = 2.48 + 2.16 + 2.48 = 96 + 32 + 96 = 224 cm2’dir.
Yanıt B
Örnek Soru
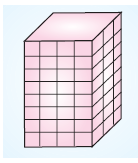
Dikdörtgenler prizması şeklindeki bir ticaret merkezinin yan yüzleri tamamıyla camla kaplanacaktır. Ticaret merkezinin tabanının uzunlukları 20 m ve 10 m’dir. Yerden yüksekliği 50m olan ticaret merkezinin camla kaplama işinin metrekaresinin maliyeti 15 TL olduğuna göre bu işin maliyeti kaç TL’dir?
![]()
Cevap
Ticaret merkezinin ön ve arka yüzü aşağıdaki gibidir.
Alan = 2.(50.20)
Alan = 2.1000
Alan = 2000 m2
Ticaret merkezinin sağ ve sol yüzü aşağıdaki gibidir.
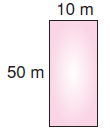
Alan = 2.(50.10)
Alan = 2.500
Alan = 1000 m2
Cam kaplanacak alan toplam
2000 + 1000 = 3000 m2’dir.
Metrekaresinin maliyeti 15 TL olduğundan
bu işin maliyeti
3000.15 = 45000 TL olur.
Yanıt C
Örnek Soru
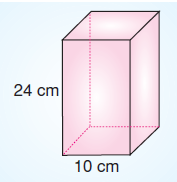
Ebru kare prizma şeklindeki kutuda satılan parfümü seçmiş ve hediye paketi yapılması için görevliye bırakmıştır.
Parfüm kutusunun taban ayrıtı 10 cm yüksekliği 24 cm olduğuna göre, görevli paketleme için en az kaç cm2 ambalaj kağıdı kullanılır?
![]()
Cevap
Parfüm kutusunun yüzey alanını bulduğumuzda kaç cm2 ambalaj kağıdı kullanılması gerektiğini bulmuş oluruz.
Üst yüzün alanı = 10.10 = 100 cm2
Alt yüz alanı = 10 . 10 = 100 cm2
Ön yüz alanı = 10 . 24 = 240 cm2
Arka yüz alanı = 10 . 24 = 240 cm2
Sağ yüz alanı = 10 . 24 = 240 cm2
Sol yüz alanı = 10 . 24 = 240 cm2
A = 100 + 100 + 240 + 240 + 240 + 240
A = 200 + 960 = 1160 cm2’dir.
O halde en az 1160 cm2 ambalaj kağıdı kullanılmalıdır.
Yanıt A
Örnek Soru
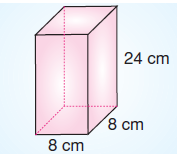
Umut, ayrıtları 8 cm, 8 cm ve 24 cm olan kare prizma şeklindeki lego parçalarıyla aşağıdaki şekli oluşturuyor.
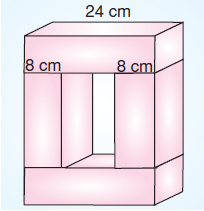
Oluşan şeklin yüzey alanı kaç cm2’dir?
![]()
Cevap
Umut lego parçalarıyla oluşturduğu parçanı
n ön yüz – arka yüz, sağ yüz – sol
yüz, üst yüz–alt yüz alanlarını bulalım.
Ayrıca şeklin içindeki yüzeylerin alanları
nı da eklemeliyiz.
Ön yüz – Arka yüz alanı bulalım.
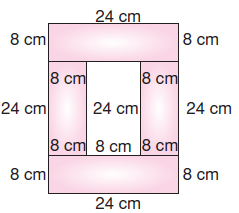
A = 24.(24 + 8 + 8) – 8.24 = 24.40 – 192 = 768 cm2
Ön yüz ve arka yüz alanı toplam 2.768 = 1536 cm2’dir.
Sağ yüz – Sol yüz alanını bulalım.
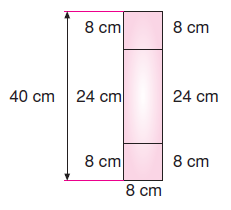
A = 40.8 = 320 cm2’dir.
Sağ yüz ve sol yüz alanı toplam
2.320 = 640 cm2’dir.
Üst Yüz – Alt Yüz alanını bulalım.
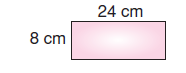
A = 8.24 = 192 cm2
Üst yüz ve alt yüz alanı toplam
2.192 = 384 cm2’dir.
İç kısımdaki yüzeyleri inceleyelim.
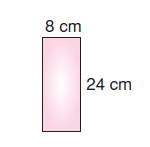
Sol taraf = Sağ taraf
Alan = 24.8 = 192
Toplam 2.192 = 384 cm2’dir.
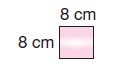
Üst kısım = Alt kısım
Alan = 8.8 = 64
Toplam 2.64 = 128 cm2’dir.
fieklin iç kısmının alanı
384 + 128 = 512 cm2 dir.
fieklin yüzey alanı
1536 + 640 + 384 + 512 = 3072 cm2’dir.
Yanıt A
Örnek Soru
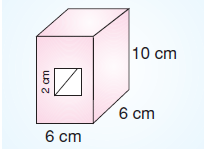
Yukarıdaki kare prizma şeklindeki bir tahtanın ortasından kare prizma şeklinde bir oyuk açılıyor.
Buna göre, bu prizmanın yüzey alanı nasıl değişir?
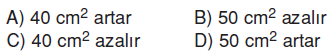
Cevap
Kare prizmanın yüzey alanını bulalım.
Ön yüz alanı = 10 . 6 = 60 cm2
Arka yüz alanı = 10 . 6 = 60 cm2
Üst yüz alanı = 6 . 6 = 36 cm2
Alt yüz alanı = 6 . 6 = 36 cm2
Sağ yüz alanı = 10 . 6 = 60 cm2
Sol yüz alanı = 10 . 6 = 60 cm2
A = 60 + 60 + 36 + 36 + 60 + 60
A = 120 + 72 + 120 = 312 cm2’dir.
Bu kare prizmanın ön ve arka yüzünden
yüzey alanı 2.2.2 = 8 cm2 olan tahta çı-
karılır.
Dış yüzey alanı ise 312 – 8 = 304 cm2
olur.
Oyuk yüzeylerinin alanı 4.2.6 = 48 cm2
olduğundan oyuk prizmanın yüzey alanı
304 + 48 = 352 cm2 olur.
O halde, yüzey alanı 352 – 312 = 40
cm2 artar.
Yanıt A
Küpün Yüzey Alanı
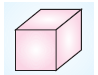
Küpün 6 yüzü vardır. Bu yüzlerin her biri birer karesel bölgedir.
Küpün tüm yüzlerinin alanları birbirine eşittir. Küpün yüzey alanı tüm yüzlerinin alanları toplamına eşittir.
Örnek Soru
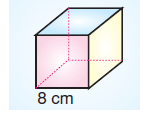
Bir ayrıtının uzunluğu 8 cm olan küpün yüzey alanı kaç cm2’dir?
Küpün bir yüzünün alanı 8.8 = 64 cm2’dir. Küpün tüm yüzlerinin alanları eşit olduğundan küpün yüzey alanı
6.64 = 384 cm2 olur.
Yanıt B
Örnek Soru
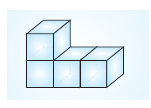
Yukarıdaki dört eş birim küpten oluşan şeklin alanı kaç birim karedir?
![]()
Cevap
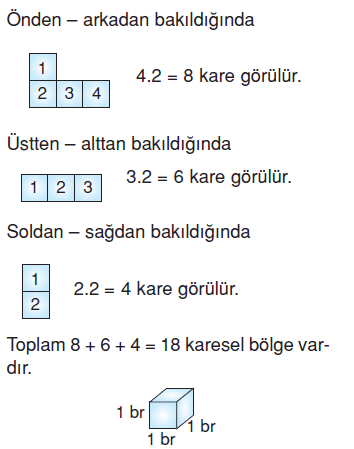
Cismi oluşturan her küpün karesel yüzeyinin alanı 1 birimkaredir. O halde verilen şeklin alanı 18 birimkaredir.
Yanıt D
Örnek Soru
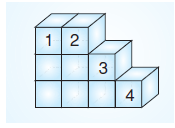
Aşağıdaki işlemlerden hangisinde yukarıda verilen cismin yüzey alanı diğerlerine göre daha büyük değer alır?

Cevap
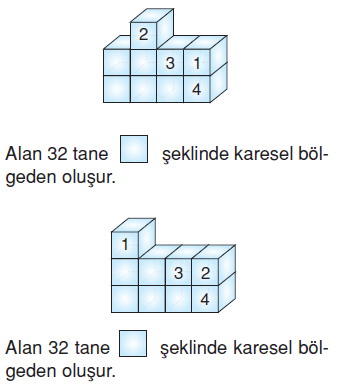
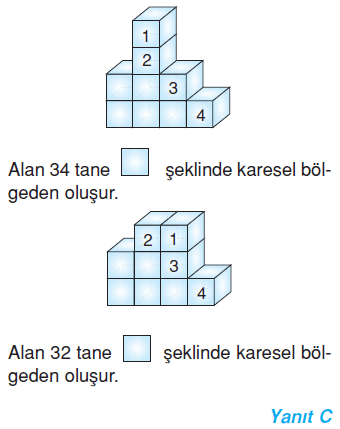
Örnek Soru
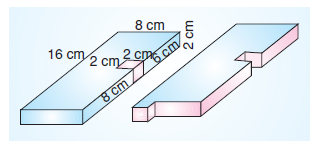
Ayrıtları 16 cm, 8 cm ve 2 cm olan dikdörtgenler prizması şeklindeki cisimden uzunluğu 2 cm olan küp şeklindeki bir parça çıkartılıp cismin ucuna şekildeki gibi ekleniyor.
Buna göre, oluşan yeni şeklin yüzey alanı kaç cm2’dir?
![]()
Cevap
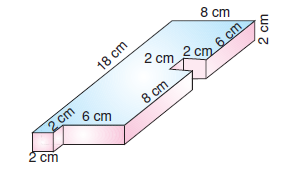
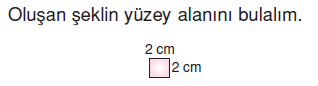
şeklindeki karesel parçalardan 5 tane
vardır. Bunların alanları toplamı
5. (2.2) = 20 cm2’dir.
Diğer parçaların alanları toplamı
2.(6+8+6) = 2.20 = 40 cm2’dir.
Sol yüzün alanı = 18.2 = 36 cm2
Arka yüzün alanı = 8.2 = 16 cm2
Üst ve alt yüzlerinde küpün üst ve alt
yüzleri çıkartılıp tekrar ekleneceği için
değişiklik yoktur.
Üst yüz alanı = Alt yüz alanı = 16.8 = 128 cm2’dir.
Oluşan yeni şeklin yüzey alanı
20 + 40 + 36 + 16 + 128 + 128 = 368 cm2
olur.
Yanıt A
Örnek Soru
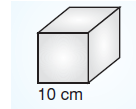
Bir ayrıtının uzunluğu 10 cm olan küp şeklindeki şeker kutuları sekizerli paketlenerek dağıtılacaktır. Kutular yan yana veya üst üste konulup paketleme kağıdıyla kaplanacaktır.
Paketleme kağıdının santimetrekaresi 0,1 kr olduğuna göre, bir paketin kaplanması için en az kaç kr’lik kağıt kullanılır?
![]()
Cevap
Kullanılacak en az kağıt için kutuların
mümkün olduğunca az yüzey alanı oluşturacak
şekilde üst üste veya yan yana
koymalıyız.
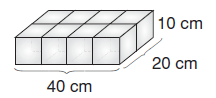
Ön yüz alanı = Arka yüz alanı = 40 . 10
= 400 cm2
Alt yüz alanı = Üst yüz alanı = 40 . 20
= 800 cm2
Sağ yüz alanı = Sol yüz alanı = 20 . 10
= 200 cm2
A = 400 + 400 + 800 + 800 + 200 + 200
A = 800 + 1600 + 400 = 2800 cm2 olur
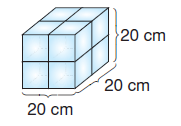
Bu ayrıtı 20 cm olan bir küp oluşur.
Küpün bir yüzünün alanı
20 . 20 = 400 cm2’dir.
Küpün tüm yüzlerinin alanı eşit olduğundan
küpün yüzey alanı
6 . 400 = 2400 cm2 olur.
Küp şeklindeki şeker kutuları üst üste
konulduğunda daha az yüzey alanı elde
edelir.
2400.0,1 = 240 kr’lik kağıt kullanılır.
Yanıt C
Örnek Soru
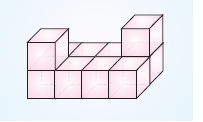
Yukarıda birim küplerden oluşan cismin alanı kaç br2’dir?
![]()
Cevap
Cismin önden, üstten ve sa¤dan görünümlerini
çizelim.
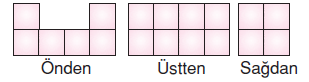
Cismin önden ve arkadan görünümleri
aynı olduğundan 2.6 = 12 birim kare,
üstten ve alttan görümleri aynı olduğundan
2.8 = 16 birim kare sağdan görünümleri
ve soldan görünümleri aynı olduğ
undan 2.4 = 8 birim kare vardır.
Toplam 12 + 16 + 8 = 36 birim kare olduğ
undan cismin alanı 36 br2 olur.
Yanıt C
Örnek Soru
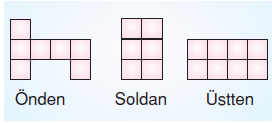
Yukarıda birim küplerden oluşmuş bir cismin farklı yönlerden görünümleri verilmiştir.
Buna göre, bu cismin yüzey alanı kaç br2 olabilir?
![]()
Cevap
Farklı yönlerden görünümleri verilen cisim
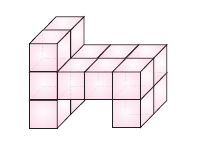
olduğundan bu cisimde bulanan birim karelerin sayısı 2.7 + 2.6 + 2.8 + 4 = 46 tanedir. O halde, cismin alanı 46 br2 olur.
Yanıt B
Örnek Soru

Yukarıda eş küplerden oluşan cismin yüzey alanı 112 cm2 olduğuna göre, bir küpün bir ayrıtı kaç cm’dir?
![]()
Cevap
Cismin farklı yönlerden görünümleri aşağıda verilmiştir.
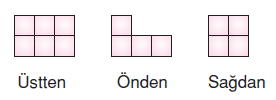
Cisimdeki toplam kare sayısı 2. (6 + 4 + 4) = 2 . 14 = 28’dir. Bir karenin alanı ![]()
O halde bir küpün ayrıtı 2 cm olur.
Yanıt C
[sinif_6_sbs_matematik]

Hiç beğenmedim .