Tüm açıları ve kenarları eş olan çokgenlere düzgün çokgen denir.
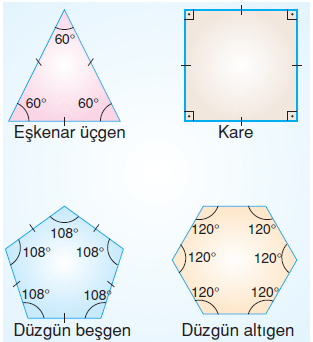
Üç kenarlı düzgün çokgene eşkenar üçgen, dört kenarlı düzgün çokgene kare, beş kenarlı düzgün çokgene düzgün
beşgen, altı kenarlı düzgün çokgene düzgün altıgen denir.
Örnek Soıru
Ece 30 cm uzunluğundaki bir teli bükerek bir kenarının uzunluğu 5 cm olan düzgün bir çokgen elde etmiştir.
Ece telin tamamını kullandığına göre, elde ettiği düzgün çokgen aşağıdakilerden hangisidir?

Cevap
Telin uzunluğu 30 cm, elde edilen düzgün çokgenin bir kenarının uzunluğu 5 cm olduğuna göre, elde edilen düzgün çokgen, 
Örnek Soru
Aşağıdaki resimlerden hangisinde düzgün çokgen modeli yoktur?

Cevap

Örnek Soru
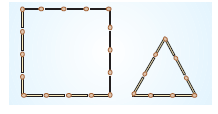
Yukarıdaki düzgün çokgenleri oluşturan kibrit çöplerinin tamamıyla aşağıdaki düzgün çokgenlerden hangisi oluşturulabilir?
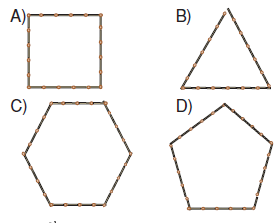
Cevap
Soruda verilen karenin bir kenarı 4 kibrit çöpünden oluştuğuna göre, karenin tamamını oluşturmak için 4 x 4 = 16 kibrit
çöpü kullanılmıştır.Üçgeni oluşturmak için ise 3 x 3 = 9 kibrit çöpü kullanılmıştır. Toplam, 9 + 16 = 25 kibrit çöpü olduğunagöre, bu çöplerin tamamıyla bir kenarı5 kibrit çöpünden oluşan düzgün beşgen oluşturulabilir.
Yanıt D
Örnek Soru
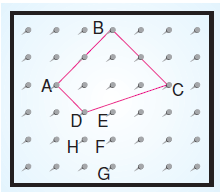
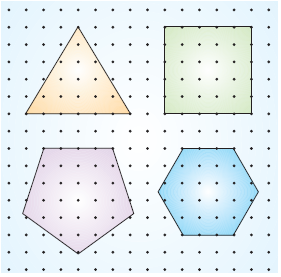
Şekildeki geometri tahtasında bazı çivilerin bulunduğu noktalar harflerle adlandırılmıştır.
Bu geometri tahtasına yerleştirilen şekildeki lastik, takılı olduğu D noktasındaki çividen çıkarılarak hangi noktadaki çiviye takılırsa elde edilen şekil bir düzgün çokgen olur?
![]()
Lastiği D noktasıdaki çividen çıkarıp farklı bir noktadaki çiviye taktığımızda düzgün çokgenlerden kare elde edilebilir. A ile B ve B ile C noktalarının arasındaki uzaklık dikkate alındığında lastik D noktasından çıkarılıp F noktasındaki çiviye takılmalıdır.
Yanıt B
Kare
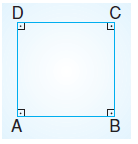
Tüm kenar uzunlukları ve tüm açıları eşit 4 kenarlı düzgün çokgene kare denir.
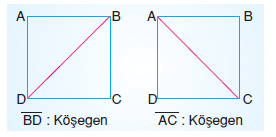
Çokgenlerde bir köşeyi komşu köşelerle birleştiren doğru parçasına kenar, karşı köşe ile birleştiren doğru parçasına köşegen
denir.
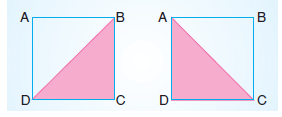
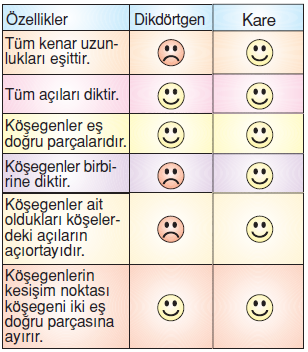
Köşegenlerin her biri karesel, dikdörtgensel ve paralel kenarsal bölgeleri iki eş parçaya ayırır.
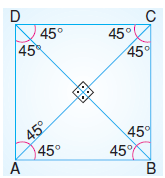
Köşegenler birbirine diktir. Aynı zamanda köşegenler ait oldukları köşelerdeki açıların açıortayıdır.
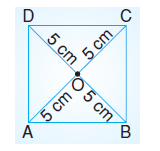
Köşegenler birbirine eşit uzunluktadır ve birbirini ortalar. O noktası karenin merkezidir.
|AC| = |BD| = 10 cm ise |OA| = |OC| = |OD| = |OB| = 5 cm olur.
Örnek Soru
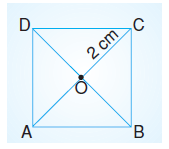
Yukarıdaki ABCD karesinde |OC| = 2 cm olduğuna göre, karenin köşegenlerinin uzunlukları toplamı kaç cm’dir?
![]()
Cevap
Köşegenler birbirine eşit uzunlukta ve birbirini ortaladıklarından;
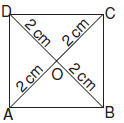
|OC| = |OD| = |OA| = |OB| = 2 cm’dir.
|AC| = |DB| = 4 cm’dir.
|AC| + |DB| = 4 + 4 = 8 cm olur.
Yanıt B
Örnek Soru
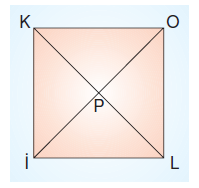
Yukarıda Ebru Hanım’ın oğluna yiyecek gönderdiği kare şeklindeki kolinin üstten görünümü verilmiştir. Koliyi köşegenlerinden geçecek şekilde iple bağlamıştır.
|Oİ| = 40 cm olduğuna göre, |PO| + |PL| + |PK| toplamı kaç cm’dir?
![]()
Cevap
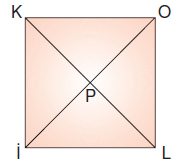
Karede köşegenlerin kesişim noktası
köşegenleri iki eş parçaya ayırır.
O halde |Oİ| = |OP| + |Pİ| ve |OP| = |Pİ| olduğundan
|OP| = |Pİ| = 40 ÷ 2 = 20 cm’dir.
|PK| = |PO| = |PL| = |Pİ| = 20 cm’dir.
|PO|+|PL|+|PK| = 20 + 20 + 20 = 60 cm
olur.
Örnek Soru
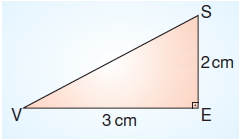
Yukarıda |VE| = 3 cm ve |SE| = 2 cm olan SEV üçgeninden mümkün olan en az sayı da kullanılarak bir kare elde ediliyor.
Buna göre, SEV üçgeninden kaç tane kullanılır?
![]()
Cevap
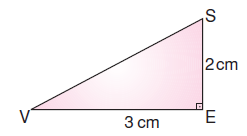
SEV üçgeni kullanılarak oluşturulabilecek en küçük karenin kenar uzunluğu EKOK(2;3) = 6 cm olur.
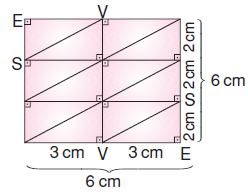
En az sayıda üçgen kullanarak oluşturulan kare yukarıdaki gibidir. 12 tane SEV üçgeni kullanılarak oluşturulur.
Yanıt D
Örnek Soru
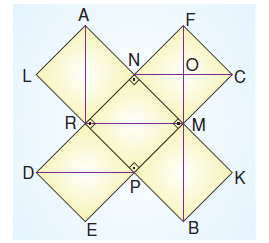
Yukarıdaki şekil 5 adet eş kareden oluşmuştur. |OC| = 2 cm olduğuna göre, |FM| + |MB| + |PD| + |MR| + |AR| toplamı kaçtır?
![]()
Cevap
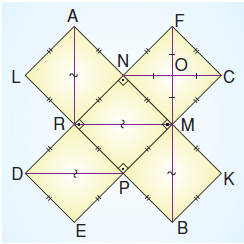
fiekildeki kareler eş olduğundan köşegenler de eştir.
|CN| = |OC| + |ON| ve |OC| = |ON| olduğundan |CN| = 2 + 2 = 4 cm olur.
|CN| = |FM| = |MB| = |PD| = |MR| = |AR| olduğundan,
|FM| + |MB| + |PD| + |MR| + |AR| = 4 + 4 + 4 + 4 + 4 = 20 cm olur.
Yanıt A
Örnek Soru
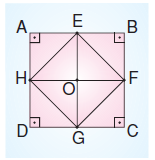
Yukarıdaki şekilde ABCD karesinin orta noktaları birleştirilmiştir. Bu ABCD karesi ile ilgili bazı öğrencilerin yorumları aşağıdaki gibidir
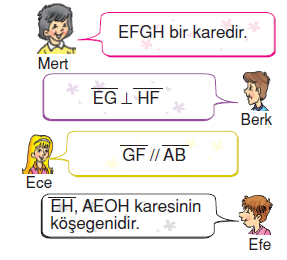
Buna göre, hangi öğrencinin yorumu yanlıştır?
![]()
Cevap
ABCD karesinin orta noktaları birleştirildiğinde EFGH karesi oluşur.
|EF| = |FG| = |GH| = |HE| ve EG // AD ve HF // AB olduğundan
EG ^ HF olur. EH, AEOH karesinin köşegenidir. O halde, Ece’nin yorumu yanlıştır.
Yanıt C
Dikdörtgen
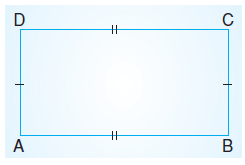
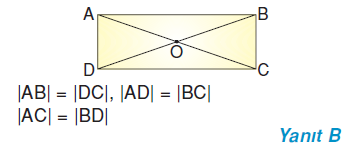
Dikdörtgenin karşılıklı kenarları eşit
uzunluktadır. |AB| = |DC| ve |AD| = |BC|’dir.

Dikdörtgenin bütün açıları 90°’dir. ![]()
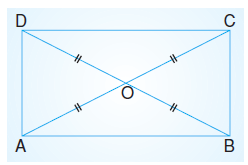
Dikdörtgende köşegen uzunlukları birbirine eşittir ve köşegenler birbirini ortalar.
|AC| = |BD| ve |OA| = |OB| = |OC| = |OD|
Örnek Soru
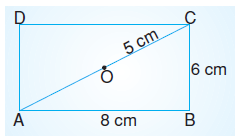
Yukarıdaki ABCD dikdörtgeninde |OC| = 5 cm, |BC| = 6 cm ve |AB| = 8 cm olduğuna göre ADC üçgeninin çevre
uzunluğu kaç cm’dir?
![]()
Cevap
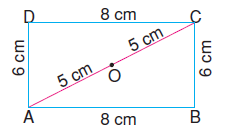
ADC üçgeninin çevresi Ç = 6 + 8 + 10 = 24 cm olur.
Yanıt C
Örnek Soru
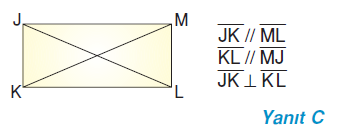
Bir JMLK dikdörtgeni için aşağıdakilerden hangisi doğrudur?

Cevap
Örnek Soru
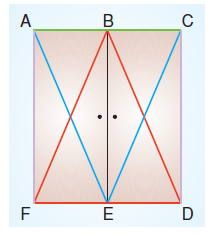
Yukarıda Ebru’nun giysi dolabının kapağı verilmiştir. Ebru dolabın sade görüntüsünden
sıkılıp dolabına renkli şeritler yapıştırıp renklendirmeye karar vermiştir. Ebru süslemede 60 cm yeşil şerit ve 96 cm mavi şerit kullanmıştır. Dolabın kapakları özdeş dikdörtgenler olduğuna göre, kaç cm kırmızı şerit kullanmıştır?
![]()
Cevap
Verilen dolapta,
Yeşil şerit : |AB| + |BC| = 60 cm ve
|AB| = |BC| olduğundan,
|AB| = |BC| = 60 ÷ 2 = 30 cm olur.
Mavi şerit : |AE| + |EC| = 96 cm ve
|AE| = |EC| olduğundan
|AE| = |EC| = 96 ÷ 2 = 48 cm olur.
Kırmızı şerit = |BF| + |FE| + |ED| + |BD|’dir.
|AB| = |BC| = |FE| = |ED| = 30 cm
|AE| = |EC| = |BF| = |DB| = 48 cm
|BF| + |FE| + |ED| + |DB| = 48 + 30 + 30 + 48 = 156 cm olur.
Yanıt C
Örnek Soru
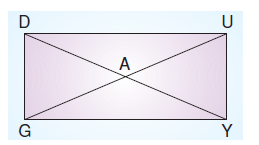
Yukarıda verilen DUYG dikdörtgeninde
GU ve DY köşegenlerdir.. |DG| = 9 cm ve |DY| = 15 cm olduğuna göre, AUY üçgeninin çevresi kaç cm’dir?
![]()

Örnek Soru
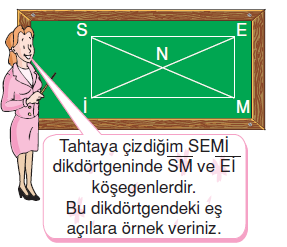
Aşağıda bazı öğrencilerin cevapları verilmiştir.
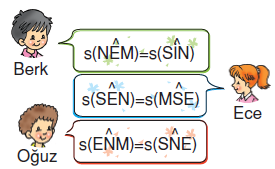
Buna göre, hangi öğrencilerin cevabı doğrudur?

Cevap
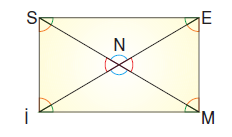
Yukarıdaki SEMİ dikdörtgenindeki eş açılar aynı renkte çizilmiştir. Öğrencilerin cevaplarını inceleyelim.
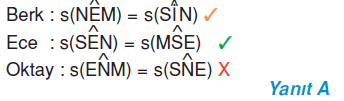
Örnek Soru
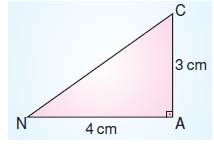
Yukarıdaki CAN dik üçgeninden kullanılarak kısa kenarı 3 cm’den büyük olan bir dikdörtgen elde edilmek isteniyor.
Buna göre, en az kaç tane üçgen gerekir?
![]()
Cevap
İki üçgeni birleştirerek aşağıdaki dikdörtgen elde edilebilir.
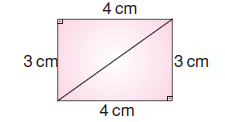
Fakat kısa kenar 3 cm’den büyük olacağından oluşturulabilecek en küçük dikdörtgen aşağıdaki gibidir.
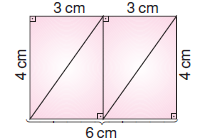
CAN üçgeninden 4 tane kullanılır.
Yanıt B
Örnek Soru
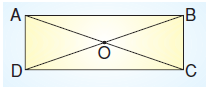
Bir ABCD dikdörtgeni için aşağıdakilerden hangisi doğrudur?

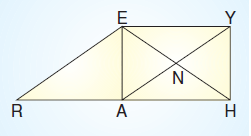
Yukarıdaki şekilde EYHA dikdörtgen, EAR dik üçgendir. |ER| = |YA| olduğuna göre, aşağıdakilerden hangisi yanlıştır?
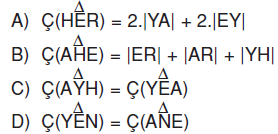
Cevap

[sinif_6_sbs_matematik]
