Uzunluk Ölçüleri

Gündelik hayatta uzunluk ölçme işlemlerinde km, m, cm ve mm ölçü birimleri daha sık kullanılır.

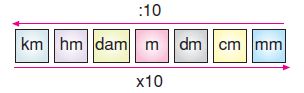
Ölçüm sonuçları arasında çevirme işleminde:
Sıralamada büyük olan birimden küçük olan birime dönüşüm yapılırken ölçüm değeri her kademede 10 ile çarpılır. Sıralamada küçük olan birimden büyük olan birime dönüşüm yapılırken ölçüm değeri her defasında 10’a bölünür.

Örnek Soru
2600 cm kaç dam’dir?

Küçük olan birimden büyük birime dönüşüm
yapıldığında ölçüm değeri her defası
nda 10’a bölünür.Bu da aşağıda gösterilmiştir.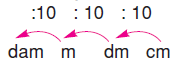

2600 : 1000 = 2,6 olduğundan,
2600 cm = 2,6 dam olur.
Yanıt B

Örnek Soru

8,83 hm kaç dm’dir?

Büyük olan birimden küçük olan birime
dönüşüm yapıldığında ölçüm değeri her
defasında 10 ile çarpılır.
0,83. 1000 =830 olduğundan
8,83 hm = 830 dm’dir.
Yanıt C

 Örnek Soru

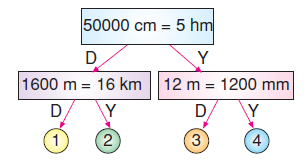
Yukarıdaki bilgi ağacındaki bilgiler doğru (D) ve yanlış (Y) olarak değerlendirilip verilen yollar takip edildi-
ğinde kaç numaralı pula ulaşılır?

Örnek Soru

Boyu 16 mm olan kalemtraşlardan kaç tanesi yan yana getirilirse kalemtıraşların boyu 4 dm olur?

Örnek Soru

I. 0,12 km = 1200 dm
II. 0,4 hm + 2,5 dam = 65 m
III. 15 cm + 0,4 dm = 0,019 dam
IV. 0,1 mm + 0,3 dm = 0,0301 m
Yukarıda verilen eşitliklerden kaç tanesi doğrudur?

Örnek Soru

Olimpiyatlara hazırlanan bir atlet 1. gün 2 km, 2. gün 24 hm koşu yapıyor. İlk üç günde toplam 7,5 km koştuğuna göre 3. gün kaç metre koşmuştur?

Atletin 1. gün ve 2. gün toplam kaç metre koştuğunu bulalım.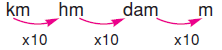

7,5 km = 7500 m
2 km = 2000 m
24 hm = 2400 m
Atlet 2 günde toplam
2000 m + 2400 m = 4400 m koşmuştur.
O halde atlet 3. gün
7500 – 4400 = 3100 m koşmuştur.
Yanıt D

Örnek Soru

Bir nalbur 40 metre uzunluğundaki duvar kağıdının 300 dm’lik kısmını metresi 4 TL’den, kalan kısmını ise metresi 5 TL’den satmıştır.Nalbur bu satıştan kaç TL kazanmıştır?

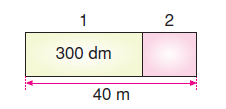
Önce 1. parçanın kaç TL’ye satıldığını bulalım.
1. parçanın uzunluğu 300 dm = 30 m’dir.
1. parça 30 x 4 = 120 TL’ye satılmıştır.
Kalan parçanın uzunluğu
40 m – 30 m = 10 m’dir.
Kalan parça ise 5 x 10 = 50 TL’ye satılmı
ştır.
Buna göre nalbur bu satıştan
120 + 50 = 170 TL kazanmıştır.
Yanıt B

Örnek Soru

Bir araba yarışı pistinin uzunluğu 6 km dir. 54 turu en kısa sürede tamamlayanın birinci olacağı yarışta yarışı tamamlayan yarışmacılar kaç m yol gitmek zorundadır?

Cevap

1 tur 6 km ise 54 turun kaç m olduğunu
bulalım.
6 x 54 = 324 km’dir. 324 km = 324000 m’ dir.
Yanıt D

Örnek Soru

Berk, internette yaptığı bir araştırmada yukarıdaki bilgilere ulaşıyor. Bu bilgiler ile ilgili arkadaşlarının yorumları aşağıdaki gibidir.

Berk’in hangi arkadaşının ya da arkadaşlarının yorumları doğrudur?

Bao Xishun’un boyu 236 cm = 23,6 dm
Can’ın yorumu doğrudur.
Deniz seviyesinden en fazla yükseklikte
yaşayanlar 5090 m = 50900 dm yüksekliğ
indedir. Ece’nin yorumu yanlıştır.
Dünya’nın en uzun demiryolu tüneli olan
Seikan bölgesindeki tünelin uzunluğu
53,9 km = 5390 dam’dir.
Gaye’nin yorumu yanlıştır.
Yanıt A

Örnek Soru

İpek, 1 dam uzunluğundaki ipi 2’şer
metrelik ipler olacak şekilde kesiyor.
Parçaların bir tanesini kendi alıp diğerlerini
arkadaşlarına veriyor.
Buna göre, İpek kaç arkadaşına ip vermiştir?

Sorunun çözümüne ulaşmak için 1 dam’ın içinde kaç tane 2 m olduğunu bulmalıyız. 1 dam = 10 m10 m : 2 m = 5 İpek 5 parça ip elde etmiştir.O halde, 5 – 1 = 4 arkadaşına ip vermiştir.
Yanıt A

Örnek Soru

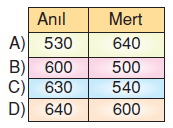
Yukarıdaki tabloda, yapılan aktivitelerle harcanan kalori miktarları verilmiştir. Anıl 1. gün 1 km yürümüş, daha sonraki günlerde bir önceki günkü mesafenin 500 m fazlası kadar yürümüştür.Mert, 1. ve 2. gün 1’er km koşmuş, 3. ve 4. gün 1’er km bisiklet sürmüştür.
Buna göre, Anıl ve Mert’in ilk dört günde harcadıkları kalori miktarları için aşağıdakilerden hangisi doğrudur ?

Örnek Soru

Ece’nin eviyle işyeri arasındaki uzaklık 15 km’dir. Sabah evden aracıyla işyerine gelen Ece,öğleden sonra işyerine 3,5 hm uzaklıktaki fuara aracıyla gidip aracıyla işyerine geri dönüyor.

Buna göre, Ece toplam kaç dekametre araç kullanmıştır?

Cevap

Ece’nin eviyle işyeri arasındaki uzaklık 15 km = 1500 dam’dir.
İşyeriyle fuar arasındaki 3,5 hm’lik uzaklığı dam cinsine çevirelim.
3,5 hm = 35 dam’dir. Ece fuara gidip geri dönüş yaptığından 2 x 35 dam = 70 dam araç kullanmıştır.
O halde Ece, 1500 + 70 = 1570 damaraç kullanmıştır.
Yanıt A

 Çevre Uzunluğu

Düzlemsel bir şeklin çevre uzunluğu kenar
uzunluklarının toplamına eşittir.
Çevre uzunluğu “Ç” ile gösterilir.

Örnek Soru

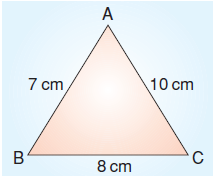
Yukarıdaki ABC üçgeninin çevresi kaç cm’dir?

Cevap

ABC üçgeninin çevresi
Ç = 7 cm + 10 cm + 8 cm
Ç = 25 cm’dir.
Yanıt B

Örnek Soru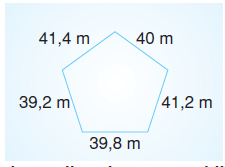

Yukarıda verilen beşgen şeklindeki parkın çevresi kaç m’dir?

Cevap
Parkın çevre uzunluğu kenar uzunlukları
toplamına eşittir. O halde;
Ç = 40 + 41,4 + 39,2 + 39,8 + 41,2 = 201,6 m’dir.
Yanıt D

Örnek Soru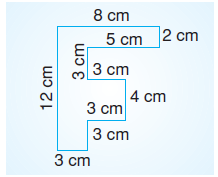

Yukarıda verilen şeklin çevresi kaç cm’dir?

Cevap

Şeklin çevresi tüm kenar uzunluklarının toplamına eşittir.
Ç = 8 + 2 + 5 + 3 + 3 + 4 + 3 + 3 + 3 + 12 olduğuna göre Ç = 46 cm’dir.
O halde, fleklin çevresi 46 cm’dir.
Yanıt A

Örnek Soru

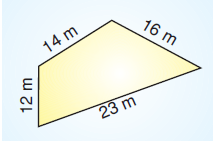
Yukarıda verilen dörtgenin çevresi kaç m’dir?

Cevap

Dörtgenin tüm kenar uzunlukları toplamı Ç = 14 + 12 + 23 + 16 = 65 m’dir.
Yanıt C

Örnek Soru

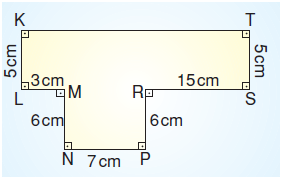
Yukarıda verilen şeklin çevresi kaç cm’dir?

Şekli aşağıdaki gibi tamamlarsak,

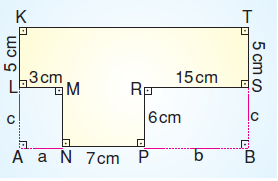
Cevap

a = |AN| = |LM| = 3 cm’dir.
b = |PB| = |RS| = 15 cm’dir.
c = |MN| = |RP| = 6 cm’dir.
|KT|= a + 7 + b = 3 + 7 + 15 = 25 cm’dir.
Ç = 25 + 25 + 5 + 5 + 6 + 6 = 72 cm dir.
Yanıt C

Örnek Soru

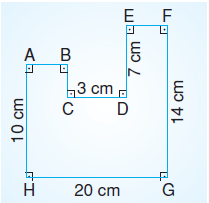
Yukarıda verilen şeklin çevresi kaç cm’dir?

Şekli aşağıdaki gibi tamamlarsak;

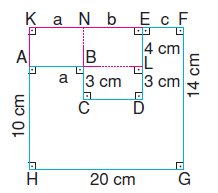
Cevap

|AB| = |KN| = a ve |CD| = |NE| = b olur.
fieklin çevresi
Ç = 10 + 20 + 14 + c + 7 + b + 3 + a’dır.
Ç = 54 + a + b + c olur.
a + b + c toplamı HG kenarının uzunlu-
ğuna eşittir.
a + b + c = 20 cm’dir.
O halde, şeklin çevresi
Ç = 54 + 20 = 74 cm’dir.
Yanıt B

Örnek Soru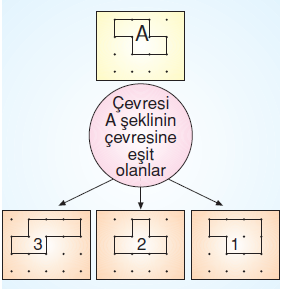

Yukarıda verilen şemada kaç numaralı şekil hatalıdır?

Cevap

Eş aralıklar sayıldığında A şeklinin çevresi 10 birim olarak bulunur. 1,2 ve 3 nolu şekillerden çevresi 10 birimden
farklı olanlar hatalı verilmiştir

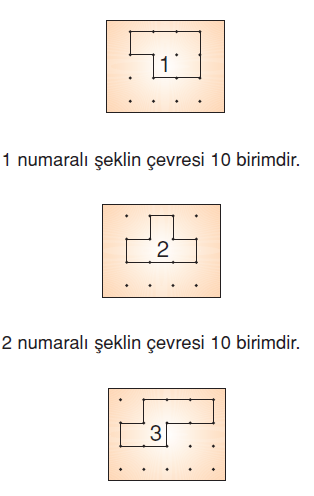
3 numaralı şeklin çevresi 12 birimdir. O halde yalnız 3 numaralı şekil hatalıdır.
Yanıt A

Eşkenar Üçgenin Çevresi

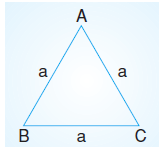
Eşkenar üçgenin çevresi bir kenar uzunluğunun üç katına eşittir. ABC eşkenar üçgeninin çevresi 3a’dır. Ç = 3.a

İki eşkenar üçgenin birleşiminden oluşan şeklin çevresi kaç cm’dir?

Cevap

Şeklin çevresi eşkenar üçgenlerin çevrelerinin toplamına eşittir.
ABC eşkenar üçgeninin çevresi Ç = 3.4 = 12 cm’dir. CDE eşkenar üçgeninin çevresi Ç = 3.6 = 18 cm’dir.
O halde, şeklin çevresi 12 + 18 = 30 cm’dir.
Yanıt C

Örnek Soru

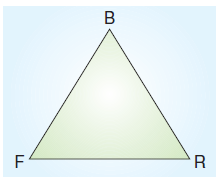
Şekilde çevresi 60 cm olan BFR eşkenar üçgeni verilmiştir. BFR üçgeninin bir kenar uzunluğu kaç cm’dir?

BFR eşkenar üçgeninin çevresi 60 cm olduğundan Ç = 3.a ise 60 = 3.a ise a=20 cm’dir. O halde eşkenar üçgeninin bir kenar uzunluğu 20 cm’dir.
Yanıt D

Örnek Soru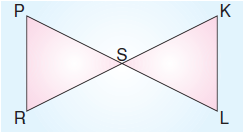

Yukarıda verilen PRS ve SKL üçgenleri eşkenar üçgenler ve |RK|= 10 cm olduğuna göre, şeklin çevresi kaç cm’dir?

|RS| = a,|SK| = b olarak kabul edersek; |PS| = |PR| = |RS| = a, |SK| = |KL| = |LS| = b olur. |RK| = a + b = 10 cm olduğundan
Ç = 3a + 3b = 3( a + b) = 3. 10 = 30 cm’dir.
Yanıt C

Örnek Soru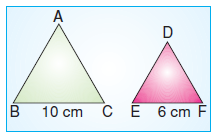

Öğretmen, çizdiği ABC ve DEF eşkenar üçgenleri ile ilgili bazı öğrencilerden yorum yapmalarını istemiştir.

Buna göre, yapılan öğrenci yorumları ile ilgili aşağıdakilerden hangisi doğrudur?

A) Yalnız Uğur’un yorumu doğrudur.
B) Yalnız Aslı’nın yorumu doğrudur.
C) Her iki yorum da doğrudur.
D) Her iki yorum da yanlıştır.

Cevap

ABC eşkenar üçgenin çevresi 3.10 = 30 cm’dir. DEF eşkenar üçgenin çevresi 3.6 = 18 cm’dir. O halde, her iki yorumda doğrudur.
Yanıt C

Karenin Çevresi

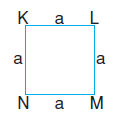
Karenin çevresi bir kenar uzunluğunun
dört katına eşittir. KLMN karesinin çevresi 4a’dır. Ç = 4.a

Örnek Soru

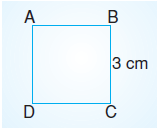
ABCD karesinin kenarlarının uzunlukları 2 katına çıkartılırsa çevresi kaç cm olur?

Cevap

ABCD karesinin kenar uzunlukları 2 katına çıkarılırsa kenar uzunluğu 3 x 2 = 6 cm olur.

Örnek Soru

Birbirine eş 16 karenin birleşimiyle yukarıdaki şekil oluşturuluyor.
Her bir karenin çevre uzunluğu 12 cm olduğuna göre şeklin çevre uzunluğu kaç cm’dir?

Cevap

Ç=4a=12 olduğundan karenin bir kenarı
3 cm’dir. fieklin çevresinde 24 tane kenar
olduğu için şeklin çevresi, 24.3=72 cm’dir.
Yanıt B

Örnek Soru

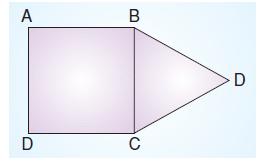
Yukarıda verilen şekilde ABCD kare ve BDC eşkenar üçgendir. Şeklin çevresi 30 cm olduğuna göre BDC üçgeninin çevresi kaç cm’dir?

Cevap

Karenin ve eşkenar üçgenin birer kenarları
ortak olduğu için kenar uzunlukları eşittir. Yani, şeklin çevresi çokgenin kenar uzunluğunun 5 katıdır.
Ç = 5.a = 30 cm ise a = 6 cm’dir. Eşkenar üçgenin çevresi Ç = 3.6 = 18 cm’dir.
Yanıt B

Örnek Soru

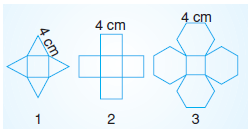
Mert, aynı karenin etrafına sırayla eşkenar üçgenler, kareler ve düzgün altıgenler çizerek yukarıdaki üç şekli elde etmiştir.
Mert’in Anıl ve Işıl adlı arkadaşlarının yorumları aşağıdaki gibidir.

Mert’in arkadaşlarının yorumları için aşağıdakilerden hangisi doğrudur?

A) Her ikisinin yorumu da yanlıştır.
B) Sadece Anıl’ın yorumu doğrudur.
C) Sadece Işıl’ın yorumu doğrudur.
D) Her ikisinin yorumu da doğrudur.

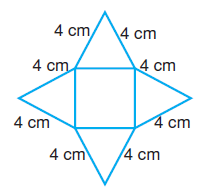
1.Şeklin çevresi 32 cm’dir.

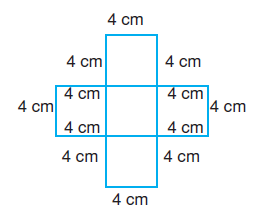
2. şeklin çevresi 48 cm’dir. 1. şekil ile 2. şeklin çevreleri eşit değildir.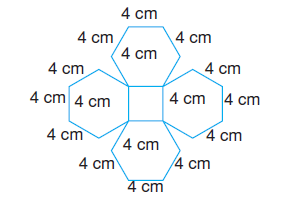

3. şeklin çevresi 80 cm’dir. 3. şeklin çevresinin uzunluğu 2. eklin çevre uzunluğundan 80 – 48 = 32 cm daha fazladır.
Yanıt C

Dikdörtgenin Çevresi

Dikdörtgenin çevresi uzun kenarının uzunluğu ile kısa kenarının uzunluğunun toplamının 2 katıdır. PRST dikdörtgeninin
çevresi 2(y + k)’dir. Ç = 2.(y+k) = 2y + 2k

Örnek Soru

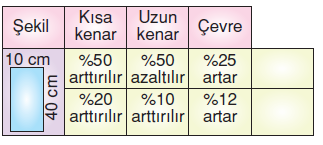
Yukarıda verilen tabloda boş kutucuklara doğru bilgi için( )  sembolü, yanlış bilgi için ()  sembolü çizilecektir.

Buna göre, aşağıdakilerden hangisi doğrudur?

Cevap

Dikdörtgenin çevresi = 2.(y+k)’dir.
Ç = 2.(40 + 10) = 100 cm’dir.
Kısa kenarı, %50 arttıralım.
Uzun kenarı, %50 azaltalım.
1. durumda,
Çevre = 2.(20 + 15) = 2.35 = 70 cm’dir.
Buna göre çevre %30 azalır.
1. bilgi yanlıştır. () Kısa kenarı, %20 arttıralım. Uzun kenarı % 10 arttıralım.
2. durumda,
Çevre = 2.(12+44) = 2.56 = 112 cm’dir.
Buna göre, çevre %12 artar. 2. bilgi doğrudur. ()

Örnek Soru

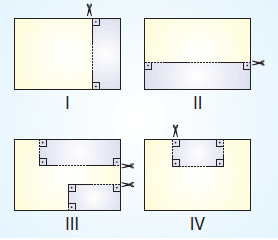
Eş dosya kâğıtları yukarıdaki gibi kesilerek boyalı parçalar atılıyor. Kalan parçanın çevre uzunluğu hangisinde en büyüktür?

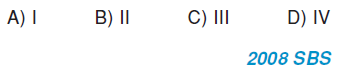
Cevap

Parçalar kesilip atıldıktan sonra,
I. şeklin çevre uzunluğu kısalttığı için azalmıştır.
II. şeklin çevre uzunluğu; kısa kenarlar
kısalttığı için azalmıştır.

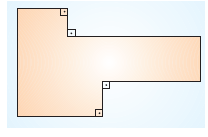
III. şeklin kesildikten sondaki hali yukarıdaki gibidir. şeklin çevre uzunluğu değişmemiştir.

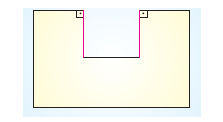
IV. şeklin kesildikten sonraki hali yukarıdaki gibidir. fieklin çevresine koyu çizilen kenar uzunlukları eklendiği için çevre uzunluğu artmıştır. O halde, IV. fieklin çevre uzunluğu en büyüktür.
Yanıt D

Örnek Soru

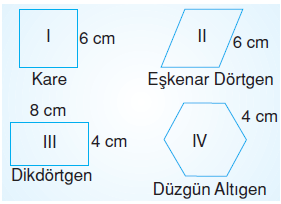
Öğretmen tahtaya yukarıdaki dört düzlemsel şekli çizmiş ve öğrencilerin bunlarla ilgili yorumlarını almıştır.

Öğretmen tahtaya yukarıdaki dört düzlemsel şekli çizmiş ve öğrencilerin bunlarla ilgili yorumlarını almıştır.

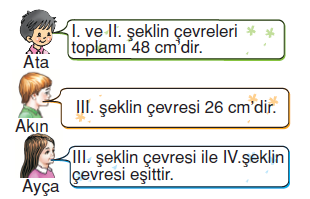
Buna göre, hangi öğrencilerin yorumları doğrudur?

Cevap

Karenin çevresi, 4 x 6 = 24 cm’dir. Eşkenar dörtgenin çevresi, 4×6=24 cm’dir. Dikdörtgenin çevresi, 2(8+4)=24 cm’dir.
Düzgün altıgenin çevresi, 6×4 = 24 cm’dir. I. ve II. şeklin çevreleri toplamı 24 + 24 = 48 cm’dir. III. şeklin çevresi 24 cm’dir. III. şeklin çevresi ile IV. şeklin çevresi eşittir.
Yanıt C

Örnek Soru

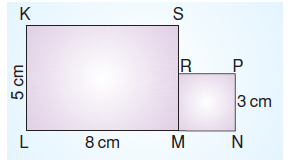
Şekilde KLMS dikdötgen ve RPMN karedir. |LM|= 8 cm, |KL|= 5 cm ve |PN|=3 cm olduğuna göre şeklin çevresi kaç cm’dir?

|KL| = |SM| = 5 cm ve |PN| = 3 cm olduğundan |SR| = 2 cm’dir.
şeklin çevresi Ç = 5 + 8 + 3 + 3 + 3 + 2 + 8 = 32 cm’dir.
Yanıt C