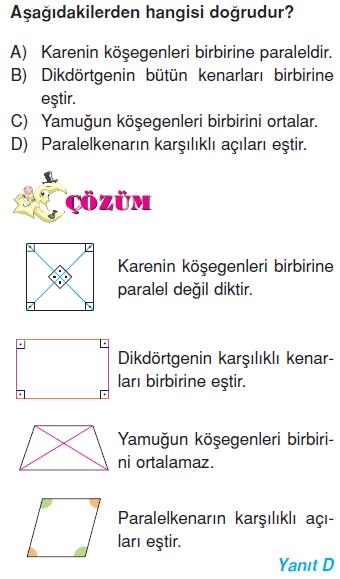
Çokgen

Doğrusal olmayan en az 3 noktanın aynı düzlemde art arda doğru parçalarıyla birleşiminden oluşan kapalı geometrik şekillere çokgen denir. İkişer ikişer kesişen doğruların oluşturduğu çokgenleri inceleyelim.

Köşegen

Çokgenlerin bir kenarının iki ucu komşu köşelerdir. Çokgenin komşu olmayan iki köşesini birleştiren doğru parçaları çokgenin köşegenleridir.

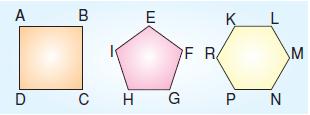
Yukarıda verilen çokgenlerin bir köşesinden geçen köşegen sayılarını bulalım.

Cevap

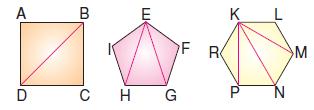
Yukarıda görüldüğü gibi dörtgenin bir köşesinden geçen köşegen sayısı 1, beşgenin 2, altıgenin 3 tanedir. Çokgenlerin bir köşesinden geçen köşegen sayısı kenar sayısından 3 eksiktir. Çünkü köşegen, komşu olmayan köşeleri birleştirdiğ inden seçilen köşenin kendisi ve 2 komşusu sayılmaz.

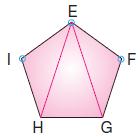
E, F, I köşelerini saymıyoruz.

Örnek Soru

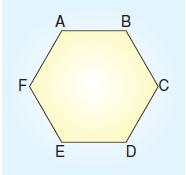
Yukarıda verilen ABCDEF altıgeninin bütün köşegenlerini bulalım.

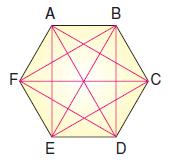
ABCDEF altıgeninin
A köşesinden (6 – 3) = 3 tane,
B köşesinden (6 – 3) = 3 tane,
C köşesinden(6 – 3) = 3 tane,
D köşesinden (6 – 3) = 3 tane,
E köşesinden (6 – 3) = 3 tane,
F köşesinden (6 – 3) = 3 tane köşegen geçer.
Ancak bu köşegenler, geçtikleri iki köşe için ikişer kere sayılır. AC köşegeni hem A hem C köşesinden, FD köşegeni hem F hem D köşesinden sayılmış olur. Bu yüzden toplam köşegen sayısı her köşeden geçen köşegenlerin toplamının yarısı kadardır.

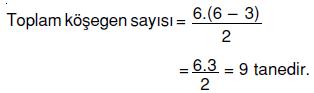
8 kenarlı bir çokgenin köşegen sayısı kaçtır?

Cevap

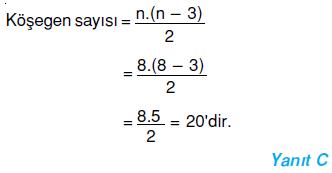
Toplam 35 tane köşegeni olan çokgen kaç kenarlıdır?

Cevap

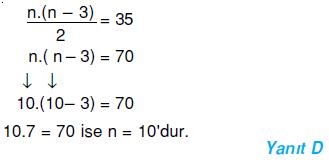
İç Bükey ve Dış Bükey Çokgenler

Bir çokgenin iç bölgesinde veya üzerinde alınan iki noktayı birleştiren doğru parçasının tamamı çokgenin iç bölgesinde kalıyorsa çokgen dış bükey aksi takdirde iç bükeydir. Yukarıdaki çokgenlerden EFGH çokgeninin üzerinde alınan A ve B noktalarını birleştiren doğru parçası çokgenin iç bölgesinde kaldığından çokgen dış bükeydir. KLMNPR çokgeninin üzerinde alınan C ve D noktalarını birleştiren doğru parçasının bir kısmı çokgenin dış bölgesinde kaldığından çokgen iç bükeydir.

Örnek Soru

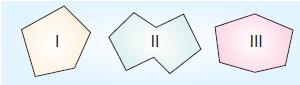
Yukarıdaki çokgenlerden hangileri dış bükey, hangileri iç bükey çokgenlerdir?

Cevap

Örnek Soru

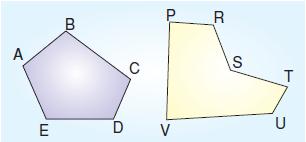
Yukarıda verilen çokgenlerin köşegenlerini çizelim.

Cevap

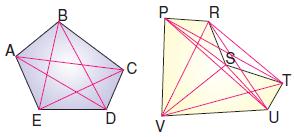
Dış bükey çokgen olan ABCDE çokgeninin bütün köşegenleri çokgenin içindedir. İç bükey çokgen olan PRSTUV çokgeninin bazı köşegenleri çokgenin dışındadır.

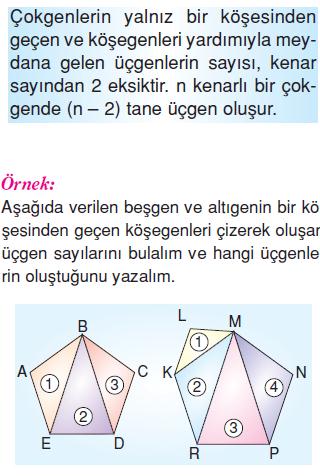
Örnek Soru

Aşağıdaki çokgenlerden hangisinin bir köşesinden geçen köşegenlerle oluşturulan üçgen sayısı 6'dır?

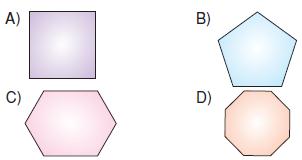
Bir köşesinden geçen köşegenlerle oluşturulan üçgen sayısı (n – 2) olduğuna göre
n – 2 = 6
n = 8 olmalıdır.
İstenilen şekil sekizgendir.
Yanıt D

Örnek Soru

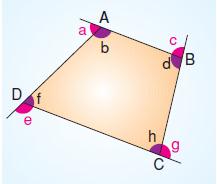
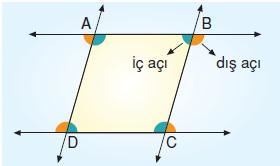
Yukarıdaki ABCD dörtgeninin iç ve dış açılarını inceleyelim.

Cevap

ABCD dörtgeninin iç aç›lar› : b, d, f, h
ABCD dörtgeninin d›fl aç›lar›: a, c, e, g'dir.
Bütünler aç›lar:
a ve b,
c ve d,
e ve f,
g ve h'dir.
a + b = 180°
c + d = 180°
e + f = 180°
g + h = 180°'dir.

Düzgün Çokgenler

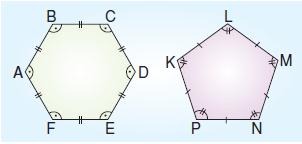
Kenar uzunlukları birbirine eşit ve açıları eş olan çokgenlere düzgün çokgen denir. Düzgün çokgenlerin merkezinden geçen köşegenler birbirlerine eştir.

Örnek Soru

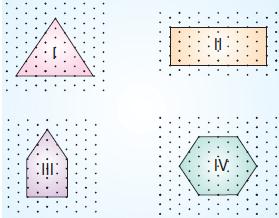
Yukarıdaki çokgenlerden kaç tanesi düzgün çokgendir?

Cevap

I ve IV numaralı çokgenlerin tüm kenarları ve açıları eş olduğundan düzgün çokgenlerdir. II numaralı çokgenin tüm açıları eştir fakat tüm kenarları eş olmadığından düzgün çokgen değildir. III numaralı çokgenin hem kenarları hem de açıları eş olmadığından düzgün çokgen değildir.
Yanıt B

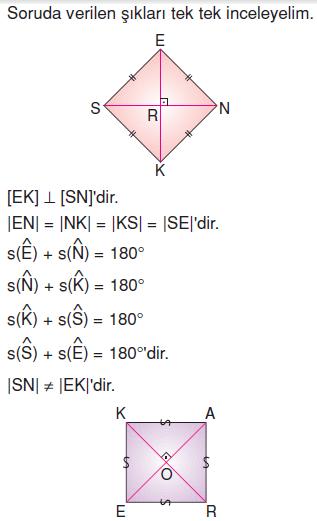
Örnek Soru

Yukarıda verilen ifadenin doğru olması için aşağıdakilerden hangisi yapılmalıdır?

Cevap

Verilen ifadenin doğru olması için K kelimesi yerine “köşegen” yazılmalıdır. İfadenin doğrusu aşağıdaki gibidir. “Bir köşesinden çizilen köşegen sayısı on olan çokgen on üç kenarlıdır.”
Yanıt C

Örnek Soru

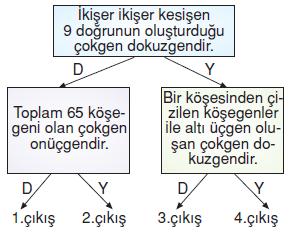
Yukarıdaki dallandırılmış bilgi ağacında verilen bilgiler doğru (D) ve yanlış (Y) olarak değerlendirilerek verilen yollar takip edilirse kaç numaralı çıkışa ulaşılır?

Cevap

“İkişer ikişer kesişen 9 doğrunun oluşturduğu çokgen dokuzgendir.” bilgisi doğrudur. Toplam 65 köşegeni olan çokgenin kenar
sayısı:

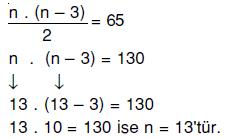
“Toplam 65 köşegeni olan çokgen onüçgendir.” bilgisi doğrudur. O halde, 1. çıkışa ulaşılır.
Yanıt A

Örnek Soru

Aslı Öğretmen'in öğrencilerinden çizmesini istediği çokgeni aşağıda defterleri verilen öğrencilerden hangisi doğru çizmiştir?

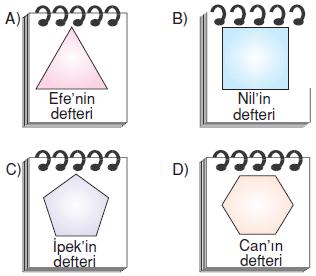
Cevap

Dörtgenler

Bir düzlemde herhangi üçü doğrusal olmayan dört noktayı birleştiren doğru parçalarının birleşimine dörtgen denir.

Dörtgen Çeşitleri 

Kare

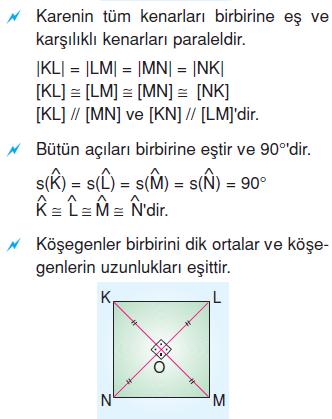
dikdörtgen

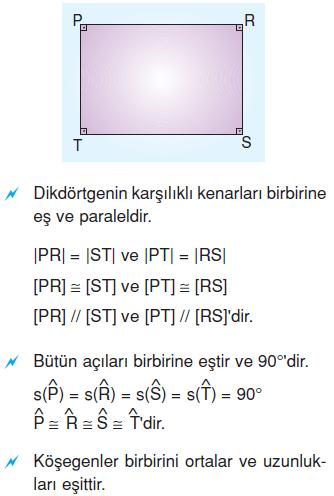
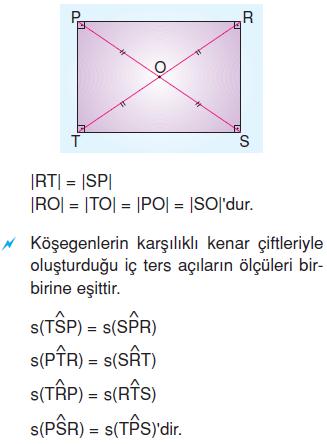
Paralelkenar

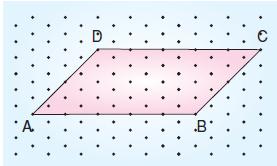
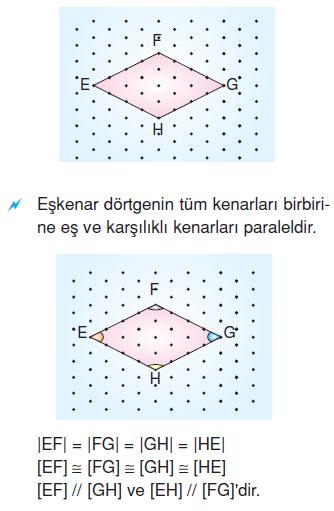
Paralelkenarın karşılıklı kenarları birbirine eş ve paraleldir.

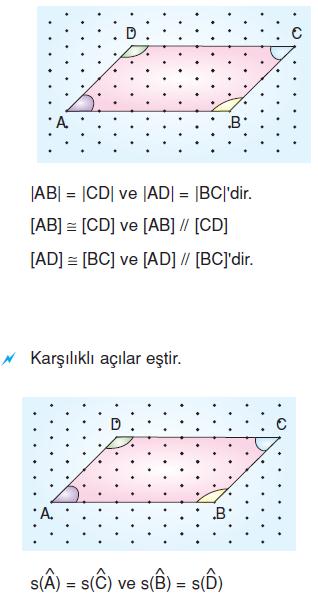
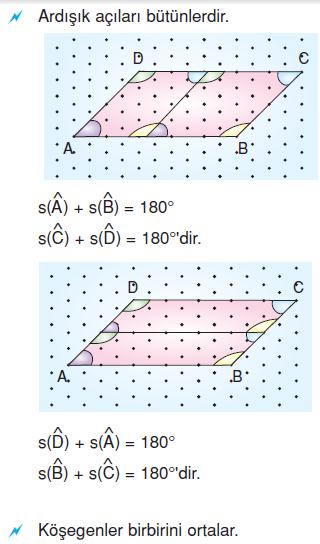
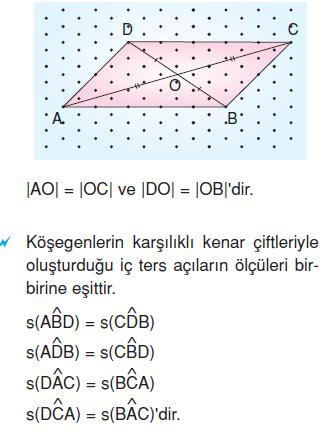
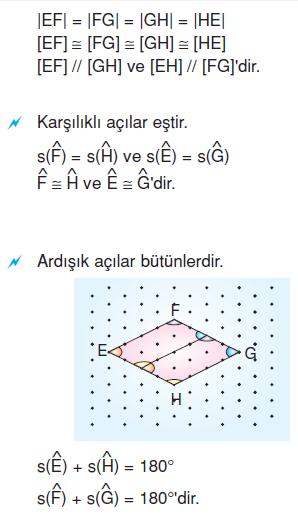
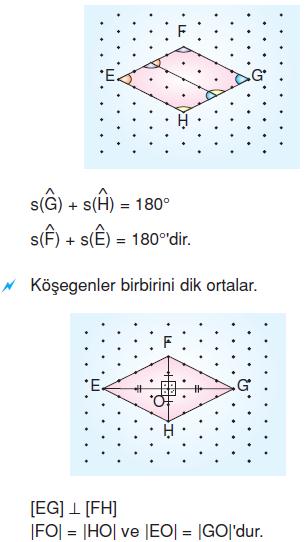
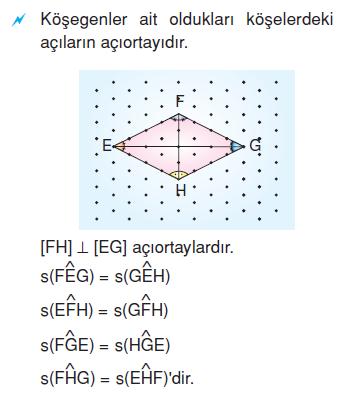
Eşkenar Dörtgen

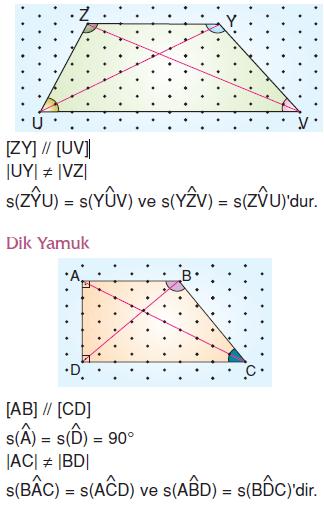
Yamuk

Örnek Soru

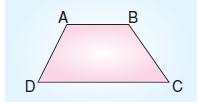
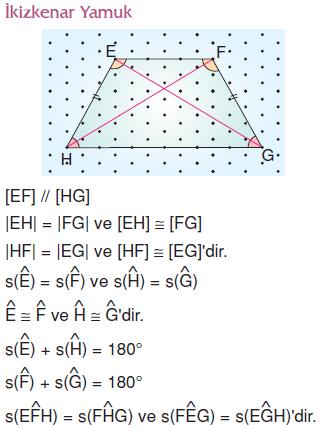
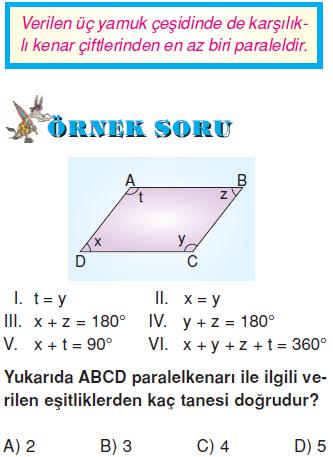
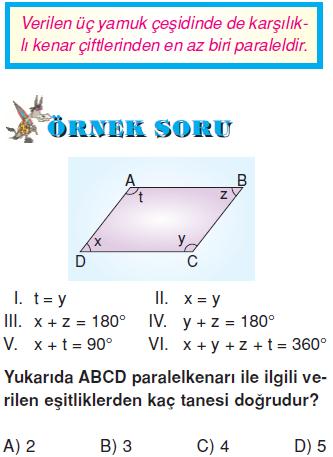
Yukarıda verilen ABCD yamuğu ile ilgili aşağıdaki özelliklerden hangisi doğrudur?

Yamuk, ikizkenar yamuk ve dik yamuk için doğru olan tek özellik karşılıklı kenar çiftlerinden en az birinin paralel olmasıdır. O halde, C şıkkında verilen özellik ABCD yamuğu için doğrudur.
Yanıt C

Örnek Soru

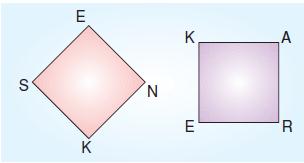
Aşağıdakilerden hangisi eşkenar dörtgen ile karenin ortak özelliklerinden biri değildir?

Cevap

Örnek Soru

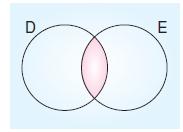
D = {Dikdörtgenin özellikleri}
E = {Eşkenar dörtgenin özellikleri}
Aşağıdakilerden hangisi yukarıdaki pembe boyalı bölgenin elemanıdır?

Cevap

Örnek Soru

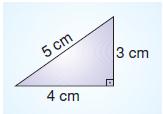
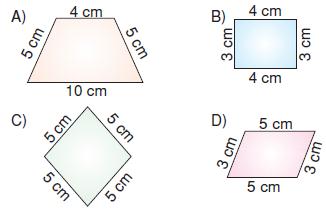
Aşağıdaki dörtgenlerden hangisi sadece yukarıdaki üçgene eş olan üçgenlerin birleştirilmesiyle oluşturulamaz?

Cevap

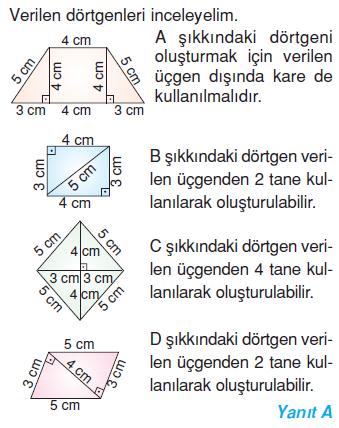
Örnek Soru

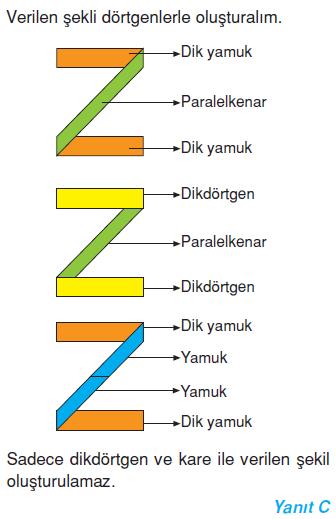
Aşağıdaki dörtgenlerden hangileri kullanılarak yukarıdaki şekil oluşturulamaz?

Cevap

Örnek Soru

Aşağıdaki dörtgenlerden hangisinin köşegen uzunlukları her zaman eşittir?

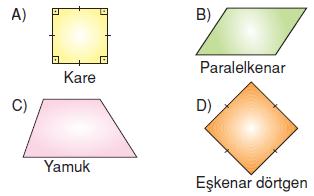
Cevap

Köşegen uzunlukları her zaman eşit olan dörtgenler kare ve dikdörtgendir.
Yanıt A

Örnek Soru

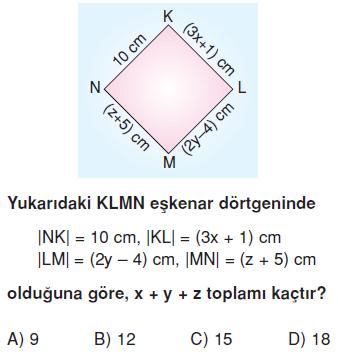
Eşkenar dörtgende tüm kenarların uzunlukları birbirine eşittir.
3x + 1 = 10 ise 3x = 9
x = 3'tür.
2y – 4 = 10 ise 2y = 14
y = 7'dir.
z + 5 = 10 ise z = 5'tir.
x + y + z = 3 + 7 + 5 = 15 olur.
Yanıt C

Örnek Soru

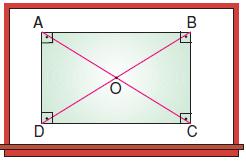
Öğretmen tahtaya bir dikdörtgen çizerek öğrencilerden yorum yapmalarını istemiştir. Öğrencilerin yaptıkları yorumlar aşağıda verilmiştir.

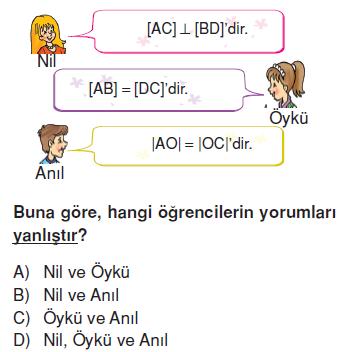
Cevap