Bir Karmaşık Sayının Kutupsal (Trigonometrik) Gösterimi

Z = a + ib karmaşık sayısına düzlemde karşılık gelen nokta K(a, b) noktasıdır.

yazılışına, karmaşık sayısının kutupsal (trigonometrik) biçimi denir.
OK doğru parçasının x ekseni ile pozitif yönde yaptığı aç0ının esas ölçüsüne Z karmaşık sayısının esas argümenti denir.

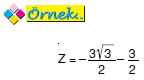
karmaşık sayısının kutupsal biçimi aşağıdakilerden hangisidir?

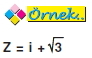
sayısının, kutupsal koordinatlarda ifadesi hangisidir?

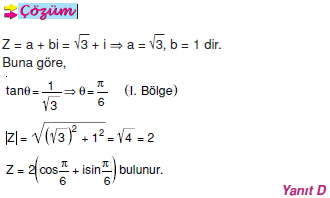
Z = 3(–cos20° + icos70°)
karmaşık sayısının esas argümenti kaç derecedir?
A) 110 B) 120 C) 130 D) 140 E) 160

Z = 3(–cos20° + icos70°)
Z = 3(–cos20° + isin20°)
Z = 3[cos(180° – 20°) + isin(180° – 20°)]
Z = 3.(cos160° + isin160°) şeklinde yazılır.
Arg(Z) = 160° bulunur.
Yanıt E

Z = x + iy olmak üzere,
|Z – 4i| = 2
eşitliğini sağlayan Z karmaşık sayılarının esas argümenti en küçük olanın esas orgümenti kaç derecedir?
A) 30 B) 45 C) 60 D) 90 E) 120

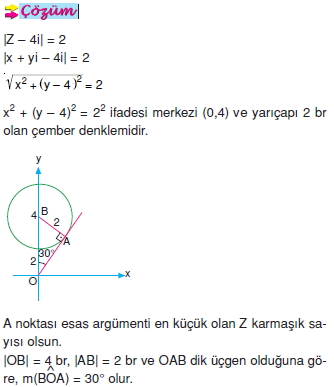
O halde, istenilen koşulları sağlayan Z karmaşık sayılarından esas argümenti en küçük olanın esas argümenti 90° – 30° = 60° dir.
Yanıt C
[matematik_2_lys]