Gaz Yasaları

Basınç – Hacim ilişkisi (Boyle – Mariotte Kanunu)

Sabit sıcaklıktaki belirli bir gazın basıncı hacmi ile ters orantılıdır.

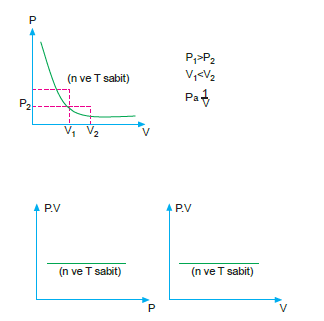
Basınç – hacim çarpımı sabit olduğundan (sabit sıcaklık ve miktarda),
P1.V2 = P2.V2 olur.
ÖRNEK: Sabit sıcaklıkta belirli bir miktar gazın hacmi 3 katına çı- karılıyor.
Buna göre, gazın basıncındaki değişme nasıl olur?
A) 3 kat azalır B) 3 kat artar C) 3 te birine düşer
D) 3 katına çıkar E) Yarıya düşer
ÇÖZÜM: Basınç – hacim ters orantılı olduğundan
P1.V1 = P2.V2
P1V = P2 . 3V eşitliğinden
P2 = P 1 olur.

Basınç üçte birine düşer
Yanıt C

Hacim – Sıcaklık İlişkisi (Charles Yasası)

Sabit basınç altında belirli bir miktar gazın hacmi ile mut- lak sıcaklığı doğru orantılıdır

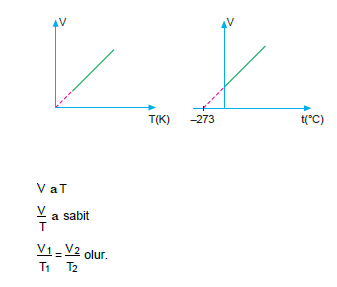
NOT: Gaz hacminin sıfırlandığı ve tüm gazların yoğunlaştığı sıcaklık – 273°C dir. Bu noktaya mutlak sıfır noktası denir.
ÖRNEK: Sabit basınçta 300 ml hacme sahip X gazının sıcaklığı –23°C ye düşürüldüğünde hacmi 200 ml olmaktadır.
Buna göre, X gazının ilk sıcaklığı kaç °C dir?
A) 34,5 B) 69 C) 102 D) 204 E) 375

Basınç – Sıcaklık İlişkisi (Gay Lussac Yasası)

Miktarı ve hacmi sabit tutulan bir gazın basıncı, mutlak sıcaklığı ile doğru orantılıdır.

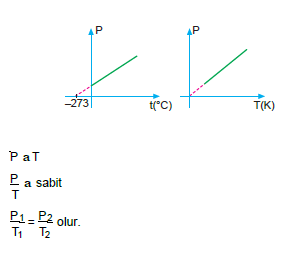
ÖRNEK: 30°C deki bir miktar gaz, sabit hacimli kapta 2 atm basınç yapmaktadır.
Sıcaklık 60° ye getirildiğinde,I. Basınç 4 atm olur.
II. Gazın özkütlesi artar.
III. Birim hacimdeki gaz tanecik sayısı değişmez.
yargılarından hangileri yanlış olur?
A) Yalnız I B) Yalnız II C) I ve II D) II ve III E) I, II ve III
ÇÖZÜM: Sıcaklık iki katına çıkmış ancak mutlak sıcaklık iki katına çıkmamıştır. (I yanlış) Kabın hacmi ve içindeki gazın kütlesi değişmeyeceğinden d = m/V eşitliğine göre özkütle değişmez. (II yanlış) Birim hacimdeki tanecik sayısı değişmez. (III doğru) Yanıt C

Mol – Hacim İlişkisi (Avogadro Yasası)

Sabit sıcaklık ve basınçtaki bir gazın hacmi mol sayısı ile doğru orantılır.

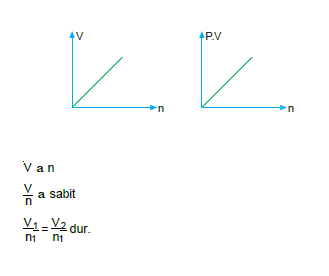
Mol – Basınç İlişkisi (Dalton Kısmi Basınç Yasası)

Sıcaklığı ve hacmi sabit olan bir gazın mol sayısı ile ba- sıncı doğru orantılıdır.

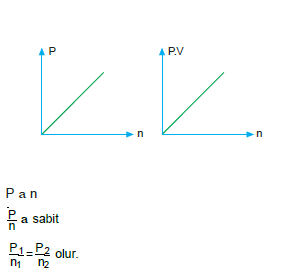
•  Kısmi basınç: Bir gaz karışımındaki her bir gazın kendi başına uyguladığı basınca denir.

PToplam= P1+ P2+ P3 …
P1/n1=P2/n2=Pt/nt

Bileşik Gaz Denklemi

Bahsedilen gaz yasaları birleştirildiğinde,

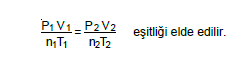
Bu eşitlik bir çok problemin çözümünde, sistemde sabit kalan değerler sadeleştirilerek kullanılır

Gazların Karıştırılması

Birleşik gaz denkleminden faydalanılarak karışan gazla- rın son basınç veya son hacmi hesaplanır