Örnek;
A(–3, 5) noktasının x eksenine göre, simetriği olan noktayı bulunuz.
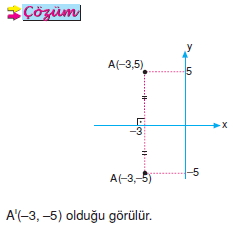
Örnek;
Simetri eksenleri x = 0 ve y = 0 doğruları olan bir dikdörtgen vardır.
Bu dikdörtgenin bir köşesi N(3, 5) noktası olduğuna göre, dört köşesinin ordinatları toplamı kaçtır?
A) – 2 B)– 1 C)0 D) 1 E) 2
Örnek;
A(–5 ,1) noktasının orijine göre, simetriğini bulunuz.
Örnek;
A(2, 3) noktasının x = 5 doğrusuna göre, simetriği olan noktayı bulunuz.
Örnek;
A(2, 3) noktasının x = 5 doğrusuna göre, simetriği olan noktayı bulunuz.
Örnek;
A(4, 1) noktasının y = –2 doğrusuna göre simetriği olan noktayı bulunuz.
Yukarıdaki şekilde, A(0, 3) noktasının B(2, 0) noktasına göre simetriği C dir.
C noktası aşağıdakilerden hangisidir?
A) (–3, –4) B) (–4, –3) C)(–4,3) D) (4, –3) E) (3, 4)
Örnek;
A(2, 6) noktasının y = x doğrusuna göre simetriği bulunuz.
Örnek;
A(–2, 3) noktasının y = –x doğrusuna göre simetriği
B ise, B noktasının y = –2 doğrusuna göre simetriği olan C noktasının koordinatı nedir?
A) (–3, –6) B) (–3, –3) C) (–6,–3) D) (6, –3) E) (–3, 6)
Çözüm;
A(–2, 3) noktasının y = –x doğrusuna göre simetriği
B(–3, 2) dir.
B(–3, 2) noktasının y = –2 doğrusuna göre, simetriği
C(–3, 2.(–2) – 2) den
C(–3, –6) bulunur.
Yanıt A
Bir doğruya göre simetriği aşağıdaki işlem basamakları izlenerek bulunur.
AA’ doğrusunun eğimi bulunur.
AA’ doğrusunun denklemi bulunur.
AA’ ile d doğrusunun kesişme noktası B bulunur.
A nın B ye göre simetriği alınıp A’ bulunur. (B yi orta nokta kabul ederek bulunuz.)
Örnek;
A(1, –1) noktasının x + y = 4 doğrusuna göre simetriği olan noktayı bulunuz.
[geometri_ygs_lys]
