Kenar uzunlukları tamsayı olan bazı dik üçgenler aşağıda verilmiştir.

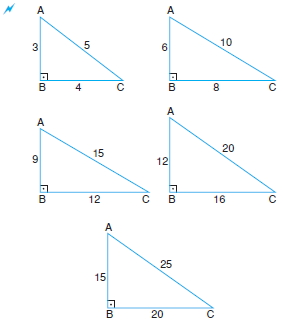
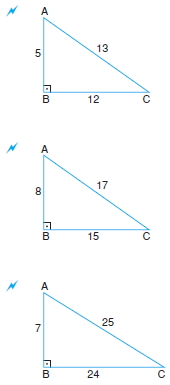
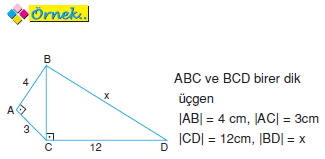
Yukarıda verilenlere göre, x kaç cm dir?
A) 5 B) 13 C) 15 D) 17 E) 20

ABC üçgeni (3 – 4 – 5) üçgenidir. |BC| = 5cm olur.
BCD üçgeni (5 – 12 – 13) üçgenidir. |BD| = x = 13cm olur.
Yanıt B

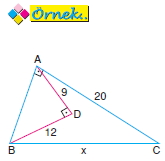ABC ve ADB birer dik
üçgen,
|AD| = 9cm
|BD| = 12cm
|AC| = 20cm
|BC| = x

Yukarıda verilenlere göre, x kaç cm dir?
A) 15 B) 16 C) 18 D) 23 E) 25

ADB üçgeni (9 – 12 – 15) üçgeni olup |AB| = 15cm bulunur.
ABC üçgeni (15 – 20 – 25) üçgeni olup |BC| = x = 25cm olur.
Yanıt E

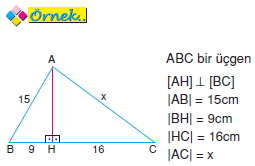
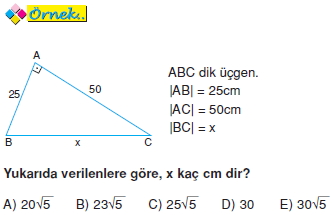
Yukarıda verilenlere göre, x kaç cm dir?
A) 15 B) 17 C) 20 D) 24 E) 25

AHB üçgeni (9 – 12 – 15) üçgeni olduğundan, |AH| = 12cm olur.
AHC üçgeni (12 – 16 – 20) üçgeni olduğundan, |AC| = x = 20cm olur.
Yanıt C

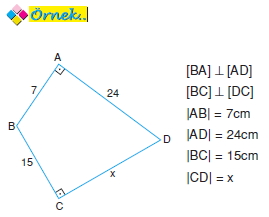
Yukarıda verilenlere göre, x kaç cm dir?
A) 25 B) 20 C) 16 D) 10 E) 8

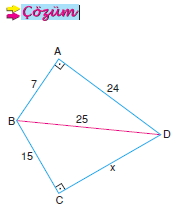
[BD] çizilirse; BAD dik üçgeni (7 – 24 – 25) üçgeni olup |BD| = 25 cm olur.
BCD dik üçgeni de (15 – 20 – 25) üçgeni olduğundan, |cd| = x = 20 cm bulunur.
Yanıt B

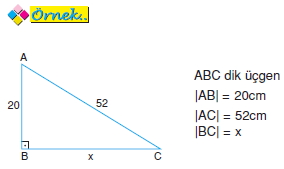
Yukarıdaki verilenlere göre, x kaç cm dir?
A) 14 B) 25 C) 30 D) 40 E) 48

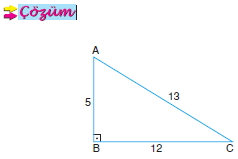
Üçgenin bütün kenar uzunlukları 4 e bölünürse yukarıdaki(5 – 12 – 13) üçgeni elde edilir.
Böylece;

|BC| = 12cm bulunur. Gerçek üçgeni elde etmek için yukarıdaki (5 – 12 – 13) üçgeninin bütün kenarlarını 4 ile çarpmak yeterli olacaktır.

Böylece, |BC| = 4.12 = 48 cm bulunur.

Yanıt E