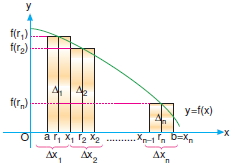
Yukarıdaki şekilde [a,b] aralığında y = f(x) fonksiyonunu kesen n tane dikdörtgen vardır.
Ardışık iç aralıklar
iç aralıklarda alınan noktaların apsisleri
ile gösterirsek bu noktalardaki ordinatlar,
olur.
Ardışık dikdörtgenlerin alanları
olduğundan bu dikdörtgenlerin alanları toplamı
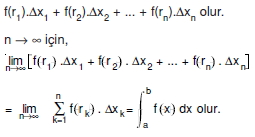
ifadesine Riemann toplamı denir.
[matematik_2_lys]