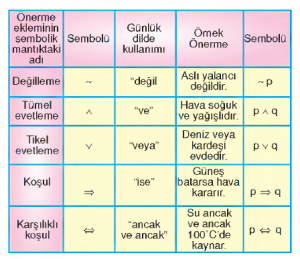
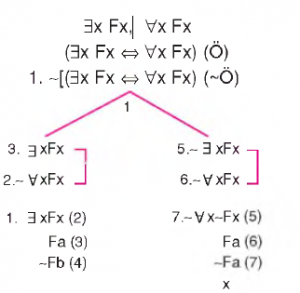Sembolik (modern) Mantık

Modern mantık, matematiksel kesinlikle hareket eden bir disiplindir. Matematiğin kesinliği, konusuna giren nicelikleri sembolleştirip bu semboller aracılığıyla işlem yapmasından kaynaklanmaktadır. Modern mantık da kendi kavramlarını sembolleştirerek son amaç olan çıkarımların geçerliliğini denetler. Sembolik Mantıkta Kullanılan Önerme Eklemleri
Önerme eklemleri, basit önermeleri birleştirerek bileşik önerme yapan mantık değişmezleridir. Ayrıca önermelerin ve çıkarımların denetlenmesini de sağlar.

•  Sembolik mantıkta semboller p, q, r, s, t şeklinde önerme eklemi almış önermeler sembolik mantıktla önerme adını alır.

Örneğin; “~p”, “p a q”,~p v ~q” gibi y Önerme eklemi almamış olanlar ise önerme adını alır. Örneğin; “p”, “q”, “r” gibi

Bileşik Önermelerin Evetleme Eklemi

a. Tümel Evetleme Eklemi

Günlük dilde iki veya daha fazla önermenin “ve”, “ile” bağlaçlarıyla bağlanarak dile getirilmesini sağlayan eklemlerdir. işareti “a ” dir.
Örneğin; “Ayşegül ve Nuray çalışkandır.” (p a q) “Ne Ayşegül ne de Nuray çalışkandır. ” (~p a ~q) “a ” eklemiyle kurulan bileşek önermelerin, doğruluk tablosunda gösterilmesi

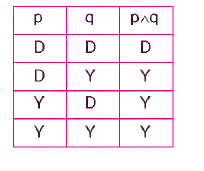
Bir tümel evetlemenin doğru olabilmesi için bileşenlerinin tümünün doğru olması gerekir. Bileşenlerden en az biri yanlış olan bir tümel evetlemenin kendisi de yanlıştır.

b. Tikel Evetleme Eklemi

iki veya daha çok önermeyi birleştiren “veya” , “ya da” gibi bağlaçlarla ifade edilen önermelerdir. işareti “v”dir. Örneğin: “Altan İzmir’e veya Antalya’ya gitti”. (p v q) “v” eklemiyle kurulan bileşik önermenin doğruluk tablosunda gösterilmesi.

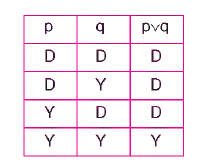
Bir tikel evetlemenin yanlış olabilmesi için bileşenlerinin tümünün yanlış olması gerekir.

c. Şart (Koşul) Eklemi

Günlük dilde “ise” , “se” , “sa” gibi sözlerle ifade edilen eklemdir. işareti ” f i ” dir. Örneğin; “Nem artarsa yağmur yağar.” (p f i q) ” f i ” eklemiyle kurulan bileşik önermenin doğruluk tablosunda gösterilmesi

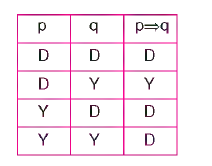
Bir koşul önermesinin yanlış olabilmesinin tek koşulu, ön bileşenin doğru, ard bileşenin yanlış olmasıdır. Bunun dışındaki her durumda koşul önermesi doğru değer alır.

d. Karşılıklı Koşul Eklemi

Günlük dilde “ancak ve ancak”ın karşılığıdır. işareti “o ” dir. Örneğin; “Murat ancak ve ancak ders çalışırsa sınavı kazanır.” ” o ” ekleminin doğruluk tablosunda gösterimi

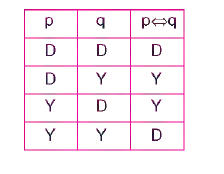
Bileşenlerin aynı doğruluk değerine sahip olduğu durumlarda karşılıklı koşullu da doğrudur.

e. Değilleme Eklemi

Günlük dilde “değil” gibi deyimlerle ifade edilir. işareti “~ ” dir. ” ~ ” in doğruluk tablosunda gösterimi

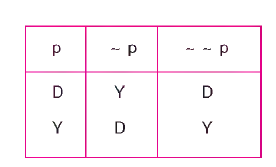
Bir önermenin değilinin değili yine kendisidir. Önermelerin Tutarlılık ve Geçerliliği Tek önermenin tutarlılığı En az bir doğrulayıcı yorumlaması olan önerme tutarlıdır.
Doğrulayıcı hiçbir yorumlaması olmayan önerme ise tutarsızdır.

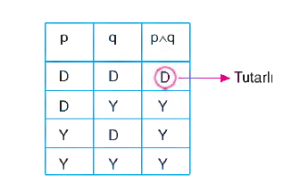
Önermeler mantığında her yorumlamada doğru olan önermeye “totoloji” her yorumlamada yanlış olan bir önermeye ise “çelişki” denir. Önermelerin Birlikte Tutarlılığı Birkaç önermenin birlikte tutarlı olabilmesi için bu önermeleri birlikte doğru kılan bir yorumlamanın bulunması gereklidir. Yani, eğer önermelerin ortak doğrulayıcı yorumları varsa tutarlıdır. Ortak doğrulayıcı yorum, doğruluk çizelgesinin aynı satırında önermelerin doğru değer almaları demektir.

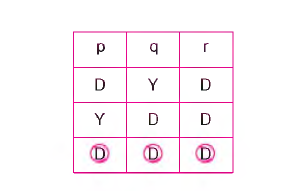
Bu yorumlama çizelgesinde son satır DDD yer aldığı için p, q, r önermeleri birlikte tutarlıdır.

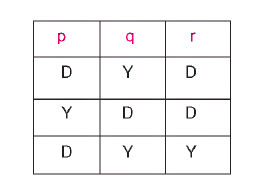
Bu yorumlamada hiçbir DDD satır olmadığı için p, q, r önermeleri birlikte tutarsızdır. Önermelerin Geçerliliği Tüm yorumları doğru olan önerme geçerlidir. Yorumlamada yanlış bulunan önerme ise geçersizdir. Geçerli olan önerme aynı zamanda tutarlı bir önerme olma özelliğine de sahiptir. Ama her tutarlı önerme geçerli değildir.

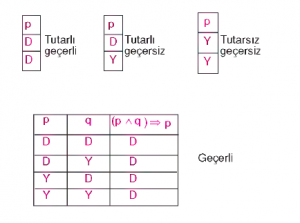
Önermelerin Eşdeğerliği

Doğruluk çizelgesinde aynı satırda aynı doğruluk değeri alan önermeler eşdeğerdir. Çıkarımların Geçerliliği Bir çıkarımın geçerli olup olmadığı denetlenirken sonuç önermesinin değilmesi alınır.
Elde edilen önermeler birlikte tutarsızsa çıkarım geçerli, tutarlı ise geçersizdir. Çıkarımların geçerliliği iki yoldan denetlenir.
I. yol:
Örneğin; q f i q ve ~p v q \ q çıkarımının geçerliliğini denetleyelim.

Denetleme sonucu öncüller ile sonucun değeili birlikte tutarlı olduğundan çıkarım geçersizdir.
II. yol:
Bu yolla denetlemede, çıkarımın öncülleri tümel evetleme eklemi (a ) ile birbirine bağlanır. Elde edilen tümel evetleme önermesi koşul eklemi ( f i) ile sonuç önermesine bağlanır. Böylece çıkarım bir koşul önermesine dönüştürülmüş olur. Koşul önermesi geçerli ise çıkarım da geçerli demektir.
Örneğin, q f i q ve p v q \ q çıkarımının geçerliliğini denetleyelim.

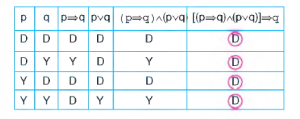
Çözümleyici Çizelge

Çözümleyici çizelge yolu ile önermeler denetlenirken iki temel kural vardır: Çatal açma ve alt alta yazma. Şimdi bu kurallara göz atalım.

Temel çözümleme kuralları

a) Tümel Evetleme

pAq, gibi bir önermenin doğru değer alabilmesinin tek koşulu vardı. Bu da her ikisinin de doğru değer almasıydı. işte bunu biz çözümleyici çizelgede alt alta yazarak ifade ediyoruz.

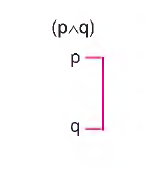
b) Tikel evetleme

pvq önermesinin doğru değer alması için bileşenlerden birinin doğru değer alması yeterlidir. Çözümleyici çizelgede bu, çatal açma kuralıyla ifade edilir.

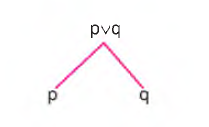
Türetilmiş Değilleme Kuralları

Türetilmiş çözümleme kuralları tümel evetleme (a) ve tikel evetleme (v) kurallarından hareketle, tümel evetleme değillemesi, tikel evetleme değillemesi, koşul, koşulun
değillemesi, karşılıklı koşul ve karşılıklı koşulun değillenmesinde uygulanır. Bu önermeler dengi olan tümel evetleme ve tikel evetlemeye dönüştürülür. Bu denkliklere De Morgan Kuralları denir. Bu denklikler şöyledir.

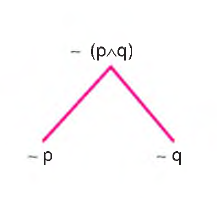
c) Tümel Evetlemenin Değillemesi

Bu işlemde çatal açılır ve önbileşen ile ard bileşenin değilleri alınır.

d) Tikel Evetlemenin Değillemesi

Bu işlemde bileşenler alt alta yazılır ve ön bileşen ile ard bileşenin değilleri alınır.

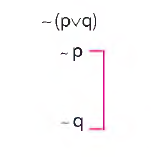
e) Koşul Önermesi

Bu işlemde çatal açılır ve ön bileşenin değili ile ard bileşenin kendisi alınır.

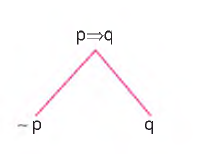
f) Koşul Önermesinin Değillemesi

Bu işlemde bileşenler alt alta yazılır ve ön bileşenin kendisi ile ard bileşenin değili alınır.

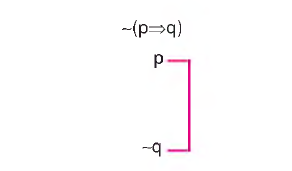
g) Karşııklı Koşul Önermesi

Bu işlemde önce çatal açılır ve açılan yollara ön bileşen ve ard bileşen alt alta yazılır. Çatalın sol tarafına bileşenlerin kendisi diğer tarafına ise değilleri alınır.

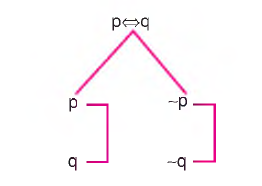
h) Karşılıklı Koşulun Değillemesi

Bu işlemde önce çatal açılır ve açılan yollarda ön ve ard bileşenler alt alta yazılır. Çatalın sol tarafına ön bileşenin kendisi ve ard bileşenin değili; sağ tarafına ön bileşenin değili ve ard bileşenin kendisi alınır.

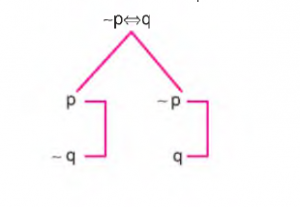
Çözümleyici Çizelgede Denetleme Kuralları

1.Ana eklem ve bileşenler belirlenir.
2.Alt alta yazma kuralına öncelik verilir.
3.Aynı kural ile çözümlenecek önerme varsa çözümlemeye en üsttekinden başlanır.

4. Çatal açmadan sonra işlem devam ediyorsa çatalın sol tarafından işleme devam edilir.
5. Alt alta yazılan önermeler dizisine yol denir. Çatal açma kuralı uygulandığında iki ayrı yol oluşur.
6. Her çözümlemeden sonra yol üzerinde çelişki olup olmadığına bakılır. Çelişki, aynı yol üzerinde hem değilinin hem kendisinin birlikte bulunmasıdır. Eğer çelişki varsa o yol x işareti ile kapatılır.
7. Çözümlenen önermelere sıraya göre adım numarası verilir. Aynı numara çözümlenmiş önermeye kaynak numarası olarak yazılır.

Bir Önermenin Tutarlılığı

Çözümleme sonunda en az bir açık yol varsa önerme tutarlıdır.
ÖRNEK:

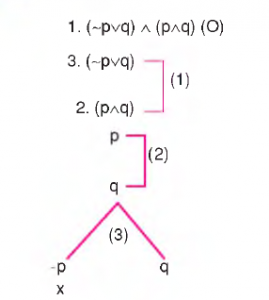
Önerme tutarlıdır.

Birden Fazla Önermenin Tutarlılığı

Birden fazla önermenin tutarlılığı, bu önermeleri birlikte doğru kılan bir yorumun bulunmasına bağlıdır. Bunun için önce önermeler alt alta yazılır ve çözümleme gerçekleştirilir.
Tek bir açık yol bile varsa önermeler birbirleriyle tutarlıdır. Önermelerin Geçerliliğinin Denetlenmesi Bu işlemde önce, verilen önermenin değili alınır ve çözümlenir. Önermenin değilinin doğrulayıcı yorumu yani açık yol varsa önerme geçersizdir.
ÖRNEK: (pA~q) f i p önermelerinin tutarlılığını denetleyelim.

Önerme geçerlidir.

Çıkarımların Geçerliliğinin Denetlenmesi

Bir işlemde çıkarımın öncülleri ile sonucun değili alt alta yazılır ve çözümleme gerçekleştirilir. Tüm yollar kapalı ise çıkarım geçerlidir. p f i r, pAq 5 r çıkarımının geçerliliğini denetleyelim.

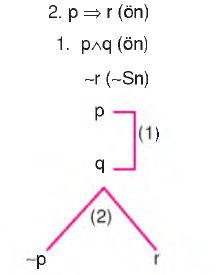
Çıkarım geçerlidir.

Önermelerin Eşdeğerliliği

Bu işlemde önermeler karşılıklı koşul (o ) eklemiyle bağlanır. Elde edilen önermenin değili alınır ve değillenmiş hali çözümlenir. Tüm yollar kapalıysa önermeler eşdeğerdir.
ÖRNEK:

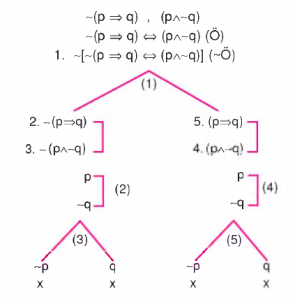
Karşılıklı koşul önermesinin değillenmiş hali tutarsız olduğu için önermenin kendisi geçerlidir. O halde bu iki önerme eşdeğerdir.

Niceleme Mantığı

Niceleme mantığında önermelerin iç yapısı da nicelikleri de çözümlemelere dahil edilir. Önermeler sembolleştirirken özne a, b, c… gibi, yüklemeler ise F, G, H gibi sembollerle gösterilir. Örneğin; “Defne çalışkandır.” önermesi “Fa” şeklinde gösterilir. Bileşik önermelerde ise yine eklemler devreye girer. Örneğin; “Öğretmen gelirse ders başlar.” önermesi “Fa f i Gb” şeklide gösterilir.

Açık Önermeler

Öznesi belli olmayan önermeler açık önermelerdir. “X mavidir.” dediğimizde önermemiz doğru ya da yanlış değer alamaz çünkü içinde değişken barındırır. içinde değişken
barından önermeler açık önermelerdir.

Özelleme

Bir açık önermeyi, önerme haline getirme işlemidir. Bunun için değişkene bir değer verilir.

Niceleyici

iki tür niceleyici vardır. Tümel niceleyici; ” sembolüyle gösteriliri. Tikel niceleyici; $ sembolüyle gösterilir.
Önermeler
Tümel niceleyici değilleme kuralı
~ “x Fx f i $x ~ Fx
Tikel niceleyici değilleme kuralı
~$x Fx f i ” x ~ Fx
NOT: Bir kurallarla aynı zamanda eşdeğerlikler de bulunmaktadır.

Özelleme Kuralları

a) Tümel Özelleme Kuralları
Çözümleyici çizelgede işlem yaparken açık bir yolda Fx gibi bir önerme varsa, o önermenin özellemesini yapmak için o yol üzerinde bulunan bir ad sembolü, eğer daha önce geçen bir sembol yoksa herhangi bir ad sembolü seçilerek değişlenin yerine koyulur ve çözümleme yapılır.
b) Tikel Özelleme Kuralı
Bir yolda $x Fx gibi bir tikel önerme varsa, bu önermenin özellemesini yapmak için, o yol üzerinde bir ad sembolü bulunup bulunamadığına bakılır. Varsa o sembolden farklı bir sembol değişkenin yerine koyulur ve çözümleme yapılır.
Çözümleme işlem Akışı
1. Tümel niceleyici değilleme kuralı
2. Tikel niceleyici değilleme kuralı
3. Alt alta yazma kuralı
4. Tikel özelleme kuralı
5. Çatal açma kuralı
6. Tümel özelleme kuralı
Önermenin Tutarlılığmm Denetlenmesi
Çözümleme sonunda en az bir açık yol varsa önerme tutarlıdır.
ÖRNEK:

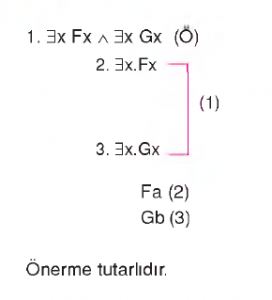
ÖRNEK:

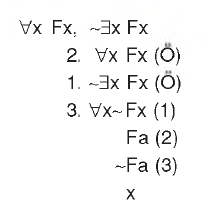
önermeler tutarsızdır.
Önermelerin Birlikte Tutarlılığının Denetlenmesi
Bu işlemde önermeler alt alta yazılır ve çözümlenir. Açık yol varsa önermeler tutarlıdır.
Önermelerin Geçerliliğinin Denetlenmesi
Bu işlemde önce önermenin değili alınır. Çözümleme sonunda
tüm yollar kapalıysa önerme geçerlidir.
Çıkarımların Geçerliliğinin Denetlenmesi
Oncüller ve sonucun değili alt alta yazılır. Çözümleme
sonunda açık yol varsa çıkarım geçersizdir.

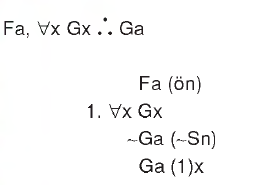
Çıkarım geçerlidir.
Önermelerin Eşdeğerliliğinin Denetlenmesi önermeler karşılıklı koşul ( f i) eklemiyle bağlanır. Elde edilen önermenin değili alınır ve değili çözümlenir. Tüm yollar kapalıysa önermeler denktir.

ÖRNEK: Aşağıdakilerden hangisi (p a q) sembolü ile gösterilir?
A) Bu deney yapılırken dikkat edilmezse patlama olabilir?
B) Bütün arkadaşları sinemaya gitmişse o da gitmiştir.
C) Yolculuğa ya otobüsle ya da trenle çıkacağım.
D) Bazı hastalıkların ortaya çıkışında kalıtım kadar beslenme de etkilidir.
E) Otobüs yahut minibüs sayısının artırılması, bu kentin ulaşım sorununu çözemez.
1993 ÖYS
ÇÖZÜM: Verilen sembol tümel evetlemedir. Buna uygun önerme D seçeneğinde verilmiştir.
Yanıt D
ÖRNEK: Aşağıdaki günlük dilde verilmiş olan önermelerin hangisinde koşul ( ^ ) eklemi yer almaz?
A) Başarılı olmak için düzenli çalışmak gerekir.
B) Başarırsın, yeter ki azimli ol.
C) Çalışmazsan başarılı olamazsın.
D) Çalış ki başarılı olasın.
E) Çok çalışmasına karşın başarılı olamadı.
1992 ÖYS
ÇÖZÜM: E seçeneğinde verilen önerme koşul önermesi değildir.
Yanıt E
ÖRNEK: Spor beden gelişimini etkiler. (p) Dengeli beslenme beden gelişimini etkiler. (q)
Buna göre, aşağıdaki önermelerden hangisi (-p a -q) biçiminde sembolleştirebilir?
A) Ne spor ne de dengeli beslenme beden gelişimini etkiler.
B) Sporun ve dengeli beslenmenin beden gelişimini etkilediği doğru değildir.
C) Spor beden gelişimini etkilemezse, dengeli beslenmede etkilemez.
D) Spor kadar dengeli beslenme de beden gelişimi için gerekli değildir.
E) Spor beden gelişimini etkilemediği zaman, dengeli beslenme etkiler.
1989 ÖYS
ÇÖZÜM: Verilen önermeler değillenmeli ve temel evetleme eklemiyle birleştirilmelidir.
Yanıt E
ÖRNEK: Günlük dilden seçilmiş aşağıdaki önermelerden hangisi tümel evetleme biçiminde değildir?
A) Zekâyı hem kalıtım hem de çevre etkiler.
B) Zekâyı ya kalıtım ya da çevre belirler.
C) Zekâyı kalıtım belirlediği gibi çevre de belirler.
D) Zekâyı kalıtım ile çevre belirler.
E) Zekâ üzerinde kalıtım kadar çevre de etkilidir.
1987 ÖYS
ÇÖZÜM: B seçeneğindeki önerme tikel evetleme (V) önermesidir.
Yanıt B