olmak üzere,

f fonksiyonu x = noktasında türevli ise f fonksiyonu x = noktasında süreklidir.

f fonksiyonu x = noktasında sürekli değil ise f fonksiyonu x = noktasında türevi yoktur.

f fonksiyonu x = noktasında sürekli ise f fonksiyonunun x = noktasında türevi olmayabilir.

f fonksiyonu x = noktasında sürekli ve bu noktada bir kırılma var ise f fonksiyonunun x = noktasında türevi yoktur.

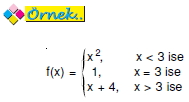
fonksiyonunun x = 3 noktasında türevinin olup olmadığını araştırınız.

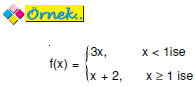
fonksiyonunun x = 1 noktasında türevinin olup olmadığını araştırınız.

olduğundan f fonksiyonu x = 1 noktasında süreklidir. f fonksiyonunun x = 1 noktasında sağdan ve soldan türevlerini araştıralım.

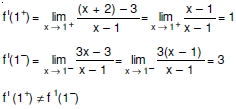
olduğundan f fonksiyonunun x = 1 noktasında türevi yoktur.

olduğundan f fonksiyonunun x = 1 noktasında türevi yoktur.

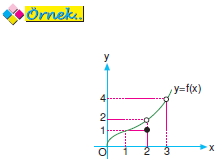
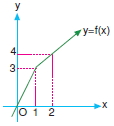
Yukarıda y = f(x) fonksiyonunun grafiği verilmiştir.
Buna göre, fonksiyonun x = 1, x = 2 ve x = 3 noktalarında türevli olup olmadığını araştırınız.

f fonksiyonu x = 1 noktasında tanımlı ve süreklidir. x = 1 noktası fonksiyonun kritik noktası olmadığından x = 1 noktasında f fonksiyonunun sağdan ve soldan türevleri eşittir. Bu yüzden f fonksiyonunun x = 1 noktasında türevi vardır.

f fonksiyonu x = 2 noktasında tanımlıdır. Fakat sürekli değildir. Bu yüzden f fonksiyonunun x = 2 noktasında türevi yoktur.

f fonksiyonu x = 3 noktasında tanımsız olduğundan x = 3 noktasında sürekli değildir ve türevi yoktur.